PID控制算法是应用非常广泛的一种控制算法,小到一个元器件的控制,大到飞机的曲线行驶、速度变化、无人机阵列等等都充斥着PID算法的身影。 PID(Proportion Integration Differentiation)其实是指比例、积分、微分控制,总的来说,当得到系统的输出后,将输出经过比例,积分,微分3种运算方式,叠加到输入中,从而控制系统的行为。
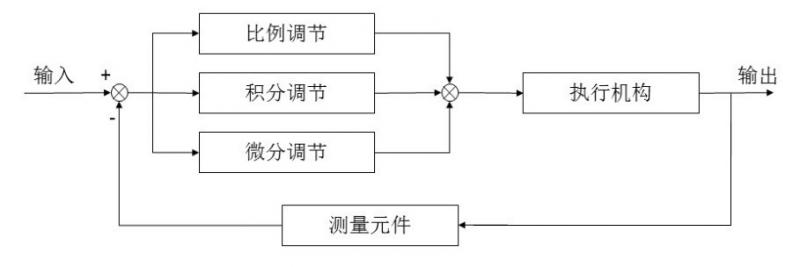
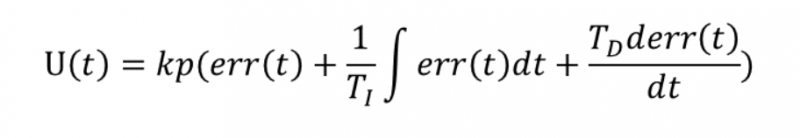
下面我们举一个很简单的例子,用比例控制算法来使水缸里的水位始终维持在1米的高度,假设水位目前处在0.2米的位置,那么当前水位(0.2m)和目标水位(1m)之间是存在一个误差(0.8m),这时,一个人通过往缸里加水来控制水位,用比例控制算法,就是指加入的水量u和误差error是成正比的。即
假设kp取0.5,那么t=1时(第1次控制系统),那么
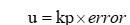
所以这一次加入的水量会使水位在0.2米的基础上上升0.4米,达到0.6米。
接着,t=2时(第2次控制),当前水位是0.6米,所以error是0.4。
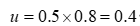
会使水位再次上升0.2米,达到0.8米,如此下去,就是比例控制的使用方法。在经过几次添加之后,水位最终会达到我们1米,但是,单纯使用比例控制算法也会存在着一些不足,其中一点就是“稳态误差”!
什么是稳态误差呢?
上述例子中,根据kp取值不同,水位最终都会达到1米,kp取值越大则上升的越快,kp取值越小则上升的越慢,不存在稳态误差。但是,假设这个水缸每次加水都会漏掉0.1米高度的水这种情况下,假设kp仍然取0.5,那么经过几次加水,水缸中的水位到0.8时,误差error=0.2. 每次往水缸中加水的量为u=0.5*0.2=0.1米,同时,缸里每加水0.1米,又会流出0.1米,也就是说,设定的目标值为1米,但是这种算法使系统水位在达到0.8米后就不再变化,由此产生的误差就是稳态误差了。
因此,单纯的比例控制,在很多时候是满足不了使用场景的。
上述例子就能看出,如果单纯的比例控制算法,会存在稳态误差,水位最终一直停在0.8米的位置上。于是,在控制中,我们再引入一个分量,该分量和误差的积分是正比关系。所以,比例+积分控制算法为:
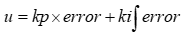
使用上述例子,第一次的误差error是0.8,第二次的误差是0.4,至此,误差的积分(离散情况下积分其实就是做累加)
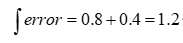
这个时候的控制量,除了比例的那一部分,还有一部分就是一个系数ki乘以这个积分项。由于这个积分项会将前面若干次的误差进行累计,所以可以很好的消除稳态误差(假设在仅有比例项的情况下,系统卡在稳态误差了,即上例中的0.8,由于加入了积分项的存在,会让输入增大,从而使得水缸的水位可以大于0.8,渐渐到达目标的1.0)这就是积分项的作用。
一辆正常行驶的汽车,发现前方红灯亮起,为了使汽车平稳行驶,很远就停止踩油门转向刹车,距离停止线越近,刹车降速会越快,直到停下来。整个过程可以看做一个加入微分的控制策略。
微分,最直白的说法就是在离散情况下,就是error的差值,就是t时刻和t-1时刻error的差,即

式中的kd是一个系数项。可以看处,在整个刹车过程中,error是越来越小的,因此微分控制项一定是负数,加入一个负数项的作用就是为了防止汽车闯过了停止线。可从常识上理解为,距离停止线越近,刹车越明显,不能让车过线。所以这个微分项的作用,就可以理解为刹车,距停止线很近时并且车速快微分项绝对值会很大。
现在在回头看这个公式,就很清楚了
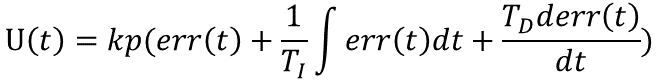
括号内第一项是比例项,第二项是积分项,第三项是微分项,前面仅仅是一个系数。很多情况下,仅仅需要在离散的时候使用,则控制可以化为
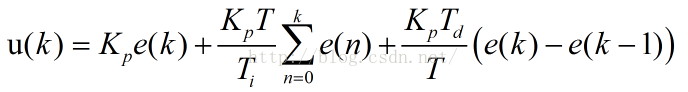
每一项前面都有系数,这些系数都是需要实验中去尝试然后确定的,为了方便起见,将这些系数进行统一:
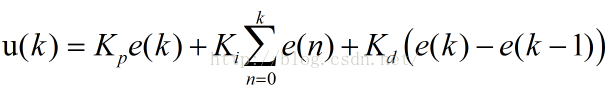
统一之后这些公式就变得清晰明了了,比例算法、微分算法、积分算法,每种算法都有个系数,直接使用这个系数回简化编程逻辑。
 芯耀
芯耀




 658
658




