最小二乘法是一种通过数值对曲线函数拟合的一种统计学方法,这里的最小是拟合误差达到最小。我们可以根据拟合后的函数可以做一些预测或预报。它在数字信号处理、机器学习等领域广泛的应用。本文W君将和大家一起学习如何通过最小二乘法进行线性回归。
我们来用一个最简单的一元线性回归模型的例子来理解最小二乘法。在生活中,我们知道人的身高和脚的大小是成正比的,这里我们假设身高和脚的大小是成一元线性关系的。那么我们怎么去建立这样一个一元线性模型呢?我们从人群中随机抽取几个身高不同的人,分别测量他们的身高和脚长,假如下面的表格就是我们的统计数据。

将他们在坐标系上显示,如下图,可以看到这些数据是趋近于一条直线的。
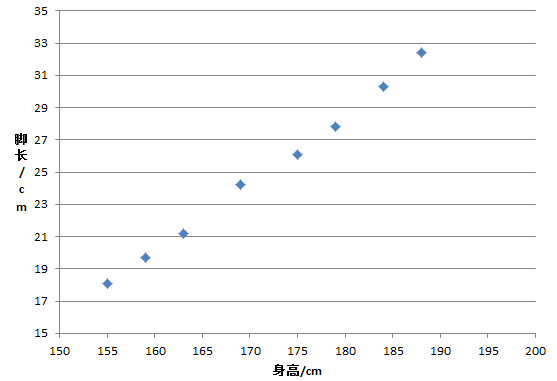
那么如何拟合这个直线呢?早在1805年勒让德就提出了最小二乘法。其方法就是根据已知的m个样本特征值,列出一个目标函数E,并求其最优解,从而使得实际值与预估值达到最小。这里的目标函数也叫损失函数,它是可以表征回归模型中估测值和真实值的不一致程度,其值越小越接近真实情况。它是由若干个预测值和真实之差的平方和构成,所以我们称之为最小二乘。
样本特征值:
![]()
目标函数:

这里我们假设拟合函数为:
![]()
这时我们的目标函数就为:
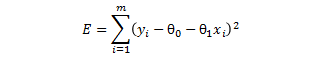
然后,通过最小二乘法使目标函数最小,求出这时的θ0和θ1的值,就可以得出拟合曲线了。
那么,问题来了?怎样让目标函数最小,求出θ0和θ1这两个参数呢? 这里我们有两种方法,对其进行求解,分别是代数法和矩阵法。
代数法
先高能预警一下,代数法公式看上去比较复杂,让人看得不免有些枯燥,W君觉得这里还是有必要列一下,大家只要理解了就好。代数法的解法就是先分别对θ0和θ1分别求偏导数,然后分别使导数为0,得到一个关于θ0和θ1的方程组,最后解方程组即可。
损失函数对θ0求导,得到方程:

损失函数对θ1求导,得到方程:

根据上面两个方程组成一个二元一次方程组,求解θ0和θ1:

类似的,对于n元一次方程也需要对每个参数进行求导,得出一个n元一次方程组,并求解出这n个θ参数。
看到这里一大堆公式是不是已经头大了?确实W君也觉得让人头大,那么,还有没有更加简洁的方法呀?这就是下面我们要学习的矩阵法了。
矩阵法
矩阵解法要比代数法简洁很多,也是大家比较习惯使用的方法。这里我们用n元一次函数作为拟合函数来求导矩阵法的公式,推导过程同样是痛苦的,但是大家最后记住公式就好,我们来看公式推导过程。
拟合函数:
![]()
其矩阵表示如下:
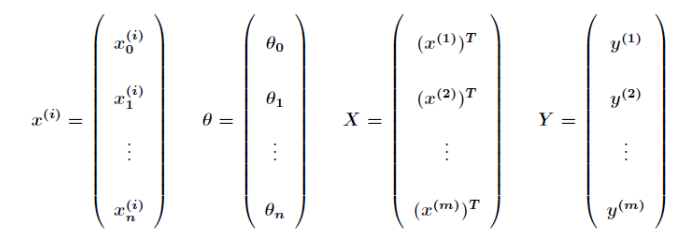
所以,损失函数:
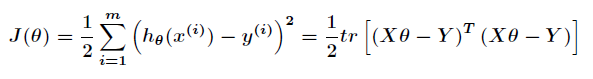
在利用矩阵的迹公式得出:
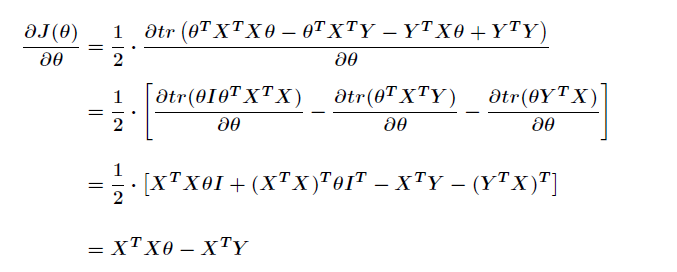
令上面的公式为0,得出:
![]()
(敲黑板,这个公式我们一定要记住!!!)
这里的θ就是我们需要求的参数,不过这里的是向量形式。
C++实现矩阵法
下面我们用矩阵法求解本文开头的例子,我们使用表格中的身高和脚长作为样本数据,再利用开源库Eigen来实现矩阵运算。关于Eigen的安装和使用可以参考W君的这篇文章《快速入门矩阵运算——开源库Eigen》。这里用到了转置函数transpose()和求逆函数inverse()。
我们来看一下求解代码,代码中利用了矩阵法求θ向量的公式。
#include <iostream>
#include "eigen_3_3_7/Eigen/Eigen"
int main()
{
Eigen::MatrixXf X(8,2);
Eigen::VectorXf Y(8);
Eigen::VectorXf result;
X << 155, 1,
159, 1,
163, 1,
169, 1,
175, 1,
179, 1,
184, 1,
188, 1;
Y << 18.1, 19.7, 21.2, 24.2, 26.1, 27.8, 30.3, 32.4;
result = (X.transpose()*X).inverse() * X.transpose() * Y;
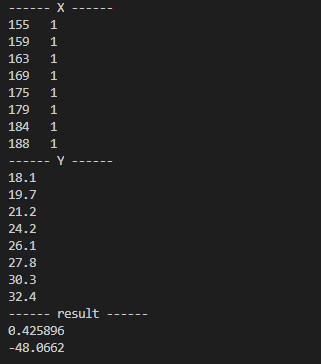
std::cout << "------ X ------" << std::endl << X << std::endl;
std::cout << "------ Y ------" << std::endl << Y << std::endl;
std::cout << "------ result ------" << std::endl << result << std::endl;
}
程序计算结果如下,θ向量两个参数分别为0.425896和-48.0662。所以,我们拟合出的曲线就是 y=0.425896x - 48.0062了 ,是不是很简单快捷?
最后,我们可以用Excel验算下我们的结果,如下图,拟合出的曲线和我们代码求出来的是一致的。
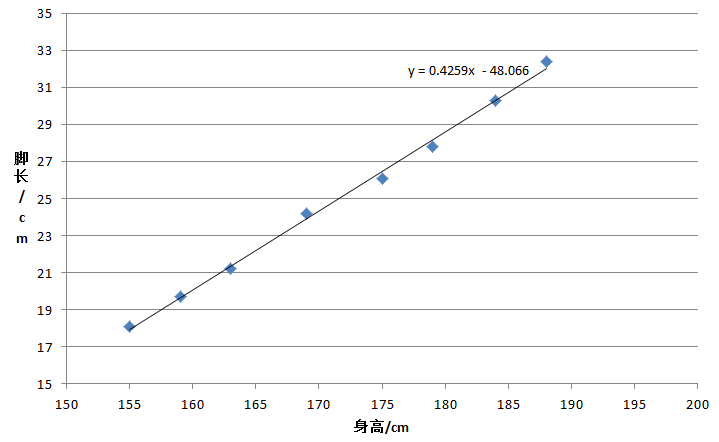
关于如何使用Excel进行曲线拟合,W君后续计划将会在Excel技巧里再为大家详细介绍,敬请关注。
 芯耀
芯耀




 3280
3280

 下载ECAD模型
下载ECAD模型






