动态规划(Dynamic Programming),简称DP,这个名字给人的感觉是一种非常高大上非常复杂的算法,很多同学看到这个名字可能就会望而却步,在面试的时候也非常害怕被问到动态规划的题目。实际上,它并不是不是一种确定的算法,它是一种最优化的方法求解问题的思想或方法。它是由美国数学家贝尔曼(Bellman)在研究多阶段决策过程的优化问题时提出。不过,与之对应的还有一些与时间无关的静态规划,如:线性规划、非线性规划等。在运筹学中,动态规划是的非常重要的内容,在各个行业领域都有着广泛的应用。我们如何理解动态规划?
如果一个问题的最优解可以通过其子问题的最优解经过推导得到,那么,我们就可以先求出其子问题的最优解,根据子问题的解得出原问题的最优解。如果子问题有较多的重复出现,为了减少重复计算,降低时间复杂度,则可以自底向上从最终子问题向原问题逐步求解并先将子问题存储起来,在求解大的子问题时可以直接从表中查询子问题的解,这就是动态规划的基本思想。
简单来来理解就是将一个大问题简化成若干子问题,并存入一个表中,再根据数据表中子问题的解求出大问题的解。这种算法看上去是不是很熟悉?其实,动态规划和分治算法类似,我们也常常将其和分治算法进行比较。它们都需要将其分解成若干子问题并求解子问题。不同的是分治算法是自顶向下求解各子问题,然后合并子问题的解从而得到原问题的解;而动态规划是将子问题拆解之后,自底向上求解子问题的解并将存储结果存储起来,在求解大的子问题时直接查询子问题的解,算法效率也将大大的提高。
理论描述太过生硬和枯燥,我们直接来看一个例子。
斐波那契数列
斐波那契数列是一个非常神奇的数列,它由意大利数学家莱昂纳-斐波那契提出,其特征是数列某一项的值是前两项的和,也可以称作黄金分割数列。
我们可以用下面的通项公式来表示斐波那契数列。
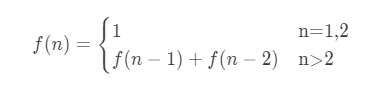
从斐波那契数列的公式中可知,数列的第n(n>2)项的值f(n)等于f(n)+f(n-1),如果要求得f(n)值就需要先求得f(n-1)和f(n-2)的值,为了便于分析,我们当假设n=6,我们可以按照下图进行分解,一步步分解成小的值。
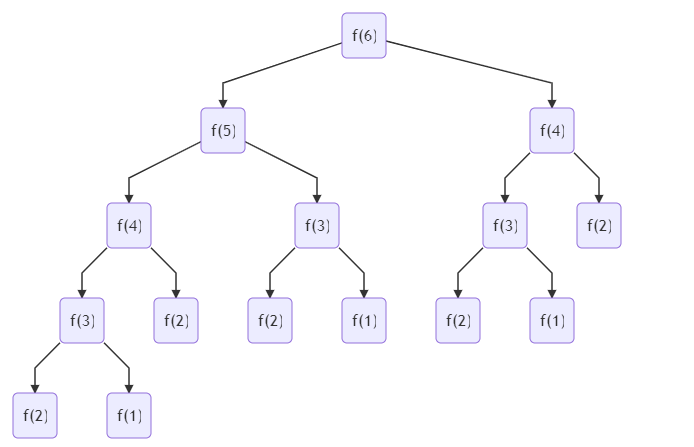
斐波那契
看了上面的图,想必大家脑海中一种想到了程序的实现,我们可以直接通过递归的方法就可以求出n项的值,程序很容易,如下所示。
int fib(int n)
{
if(n==1 || n==2) return 1;
return fib(n-1) + fib(n-2);
}
但是,很明显这种算法是指数时间复杂度O(2^n),其复杂度会随着n的增加成指数增长,当n取到一定大时,将需要很长的时间,显然这不是一种最优的算法。不过,仔细观察上图的各个分解项,我们会发现图中有很多重复的子项,这就是上面这种递归算法复杂度较高的原因。那么,还能不能进行优化呢?答案是肯定的。
我们可以通过动态规划的思想来优化上面这个算法,为了避免大量的重复计算,我们可以从最底层的子问题开始计算,并通过一个表来存储这些子问题的值,当再次遇到这个值就不需要再重新计算。
如下面的程序,我们从最小的子问题n=1,2开始向上计算,并且定义了一个vector容器用来存储被计算过的子问题的值,下次再计算大问题时直接调用容器里的值即可。
int fib(int n)
{
vector<int> dp(n, 0);
dp[0] = dp[1] = 1;
for (int i = 2; i < n; i++)
{
dp[i] = dp[i - 1] + dp[i - 2];
}
return dp[n-1];
}
很明显上面的这种算法,大大降低了算法的时间复杂度,现在的时间复杂度就是O(n)了。不过,虽然时间复杂度降低了,这却是牺牲了空间换取过来的。实际上我们还可以进一步去优化,从公式上我们分析可以看出,要求出某一项的值我们需要先求出其前两项子问题的值,当我们自下而上求解子问题的过程中,我们直接保存连续两项子问题的值即可。
int fib(int n)
{
int dp[2]={1,1};
for (int i = 2; i < n; i++)
{
int tmp = dp[0];
dp[0] = dp[1];
dp[1] = dp[1] + tmp;
}
return dp[1];
}
最长上升子序列
严格意义上来说,上面的斐波那契数列也不完全算是动态规划问题。因为从动态规划的定义上来看,动态规划问题一般满足三个性质:
- 最优化原理:如果原问题的最优解所分解出的子问题的解也是最优的,我们就称该问题具有最优子结构,原问题的最优解可以由子问题的最优解推导得出;
- 无后效性:某阶段状态一旦确定,这个状态以后决策的影响,它只与当前状态有关;
- 有重叠子问题:子问题可能会在下一阶段决策中被重复多次用到。
根据动态规划问题的这三个性质我们再看另外一个例子,最长上升子序列(Longest Increasing Subsequence)问题,简称LIS,这是一个非常经典的动态规划问题。
有一个长度为n的数列a0, a1, ..., a(n-1),求出这个序列中最长的上升子序列的长度。所谓上升子序列指的是对于任意的i<j都满足a(i)<a(j)的子序列。例如,一个序列为{6, 3, 5, 4, 7, 8, 1, 10},那么,它的最长上升子序列为{3, 5, 7, 8, 10}或{3, 4, 7, 8, 10}。
我们先将原问题进行分解,依次拆解成子问题,如下表:
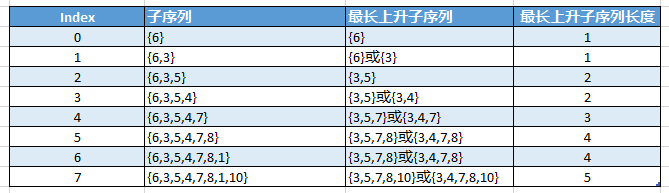
子序列
我们的代码可以按照下面来实现,其中,程序里我们用dp数组保存各个子序列以nums[i]结尾的最长子序列长度,max存储最长子序列的长度。
int maxLIS(std::vector<int>& nums)
{
int max = 1;
std::vector<int> dp(nums.size(), 1);
for(int i = 1;i< nums.size(); i++)
{
for(int j=0; j<i; j++)
{
if(nums[i]>nums[j])
{
dp[i] = dp[j] + 1;
}
max = std::max(dp[i], max);
}
}
return max;
}
通过上面的两个例子,大家都学废了吗?常见的还有很多问题可以使用动态规划的方法解决,比如,背包问题,硬币找零,最短路径等。动态规划不是一种固定的算法,对应的问题也是多种多样,但大家只要掌握了其基本的思想,就可以轻松的解出相应的问题,大家赶快去尝试一下吧!
 芯耀
芯耀




 1121
1121

 下载ECAD模型
下载ECAD模型






