复数称Complex Number,从英文上来看似乎它是“复杂的数”。其实并不然,它实际上指的是复合数,即由实部和虚部复合而成的数。它可以用下面的公式表示:
a(Real part)+ib(Imaginary part)
这里,纯实数a是实部,ib是虚部,其中,a b都是实数,i是虚数。
如果我们将实部作为x轴,虚部作为y轴,复数就可以在坐标轴上表示了,这样的坐标系我们称作复数坐标系。它和复平面上原点的连线可以表示一个向量,向量和x轴的夹角为复数的辐角theta。
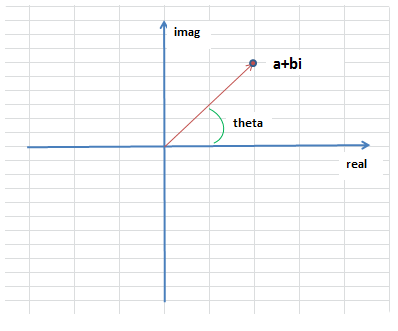
实数我们大家都很熟悉,在平时生活中,常用的也都是一些实数。那么,虚数是什么呢?
虚数并不是单纯的数字,如果x^2=-1,我们就将它们的解定义为+/-i,这里的i就是虚数,很显然虚数似乎并不是我们平时所使用的数,因为在我们所理解的实数领里任何一个数进行平方之后都不可能是小于0的,但这并代表它没有意义,我们可以换一个角度来理解虚数,我们通过它可将实数扩展到复数域。
要理解虚数我们就需要先复习一下之前学习的欧拉公式:
![]()
如果,

则,
![]()
相信这里大家应该有了发现:
![]()
在复数域中,
复数与复指数相乘,相当于复数对应的向量旋转对应的角度。
这里就相当于我们把1逆时针旋转90度,就可以得到i,如果我们再逆时针旋转90度就是-1,也就是i*i。
所以,大家也就明白了i的含义,以及为什么i的平方等于-1了。
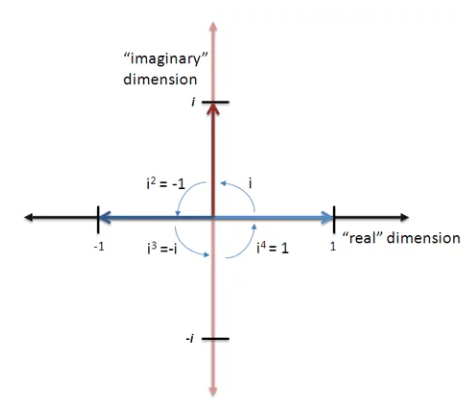
因此,虚数i的几何意义上是一个旋转量。
数学是一个伟大的工具,从实数到复数的扩展是一个里程碑的进步。数学家雅克·阿达马说,在实数域中,连接两个真理的最短的路径是通过复数域。
程序中如何定义复数?
在C++中,complex头文件中定义了一个complex模板类型,用来处理复数。格式如下:
template <class T> class complex;
template<> class complex<float>;
template<> class complex<double>;
template<> class complex<long double>;
T是实部和虚部的数字的数据类型,它可以支持float、double、long double这几种类型。
复数这个类模板有多个构造函数:
complex( const T& re = T(), const T& im = T() );
complex( const complex& other );
template<class X > complex( const complex<X>& other);
从上面复数的构造函数可以看出,我们可以用下面的几种方法来定义一个复数:
- 根据实部和虚部的值来构造一个复数;
- 根据一个复数的值来构造一个复数;
- 从不同类型的复数构造一个复数。
#include <iostream>
#include <complex>
int main ()
{
std::complex<float> z1(1.2, 2.3);
std::complex<float> z2(z1);
std::complex<double> z3(z2);
std::cout << z3 << 'n';
return 0;
}
结果输出:
(1.2,2.3)
复数的运算
复数和实数一样是可以进行+ - × /等算术运算的。假如有两个复数z1和z2,如下:
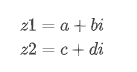
复数的加法是将两个复数的实部和实部相加,虚部和虚部相加:
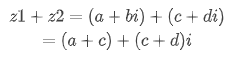
同样的,复数的减法是将两个复数的实部和实部相减,虚部和虚部相减:
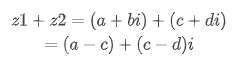
复数的乘法呢?因为复数也是满足实数域的交换律、结合律以及分配律这些定理,因此,我们可以对乘法进行分解。
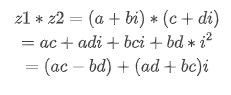
除法就会复杂一些,我们需要考虑将分母的复数转成实数。该怎么进行转换呢?在这之前,我们需要先了解共轭复数,如果有两个复数z2=c+di和z3=c-di,他们实部相同,虚部互为相反数,我们称它们互为共轭,z2是z3的共轭复数,z3也是z2的共轭复数。
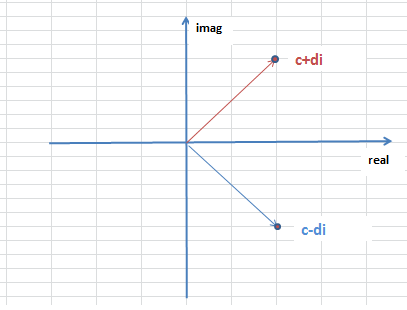
共轭
共轭复数有这样的一个特性,如果两个共轭复数相乘,它们的结果是一个实数。
因此,我们可以利用共轭复数的这个特性进行复数的除法运算。
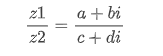
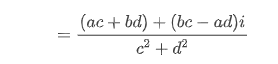
实际上,我们在使用C++写程序时不需要这么复杂的公式计算,complex类实际上已经进行重载了这些操作。
complex& operator= (const T& val);
template<class X> complex& operator= (const complex<X>& rhs);
template<class T> complex<T> operator+(const complex<T>& lhs, const complex<T>& rhs);
template<class T> complex<T> operator+(const complex<T>& lhs, const T& val);
template<class T> complex<T> operator+(const T& val, const complex<T>& rhs);
template<class T> complex<T> operator-(const complex<T>& lhs, const complex<T>& rhs);
template<class T> complex<T> operator-(const complex<T>& lhs, const T& val);
template<class T> complex<T> operator-(const T& val, const complex<T>& rhs);
template<class T> complex<T> operator*(const complex<T>& lhs, const complex<T>& rhs);
template<class T> complex<T> operator*(const complex<T>& lhs, const T& val);
template<class T> complex<T> operator*(const T& val, const complex<T>& rhs);
template<class T> complex<T> operator/(const complex<T>& lhs, const complex<T>& rhs);
template<class T> complex<T> operator/(const complex<T>& lhs, const T& val);
template<class T> complex<T> operator/(const T& val, const complex<T>& rhs);
template<class T> complex<T> operator+(const complex<T>& rhs);
template<class T> complex<T> operator-(const complex<T>& rhs);
complex头文件中已经包含了常见的运算操作,我们通过下面的的例子来加深了解。
#include <iostream>
#include <complex>
int main ()
{
std::complex<double> z1(1, 2);
std::complex<double> z2 = std::complex<double>(3, 4);
std::cout << "z1: " << z1 << std::endl;
std::cout << "z2: " << z2 << std::endl;
std::cout << "z1+z2: " << z1+z2 << std::endl;
std::cout << "z1-z2: " << z1-z2 << std::endl;
std::cout << "z1*z2: " << z1*z2 << std::endl;
std::cout << "z1/z2: " << z1/z2 << std::endl;
std::cout << "z1+2: " <<z1 + 2.0<< std::endl;
return 0;
}
上面的例子中,我们可以使用=直接对复数进行赋值操作,还可以使用运算符对复数进行运算,而且也支持实数和复数之间的运算,其输出结果如下:
z1: (1,2)
z2: (3,4)
z1+z2: (4,6)
z1-z2: (-2,-2)
z1*z2: (-5,10)
z1/z2: (0.44,0.08)
z1+2: (3,2)
当然,除了上面的运算,还支持+= -= *= /=等这些运算。
complex& operator+= (const T& val);
complex& operator-= (const T& val);
complex& operator*= (const T& val);
complex& operator/= (const T& val);
template<class X> complex& operator+= (const complex<X>& rhs);
template<class X> complex& operator-= (const complex<X>& rhs);
template<class X> complex& operator*= (const complex<X>& rhs);
template<class X> complex& operator/= (const complex<X>& rhs);
同样的,我们看下面的代码:
#include <iostream>
#include <complex>
int main ()
{
std::complex<double> z1(1, 2);
std::complex<double> z2 = std::complex<double>(3, 4);
z1 += 2.0;
z2 -= z1;
std::cout << "z1: " << z1 << std::endl;
std::cout << "z2: " << z2 << std::endl;
return 0;
}
上面的代码执行结果:
z1: (3,2)
z2: (0,2)
一些其他函数
除了上面的一些运算,complex头文件里还有一些函数,我们选择一些常见的函数来进行介绍。
- real和imag函数
- abs函数
- conj函数
- arg和polar函数
- norm函数
- exp函数
real和imag函数
我们知道了复数有实部和虚部组成,当我们需要分开对实部和虚部处理的时候,如何取得实部和虚部的值呢?
complex头文件定义了获取实部(real函数)和虚部(imag函数)的函数:
template<class T> T real (const complex<T>& x);
template<class T> T imag (const complex<T>& x);
示例:
#include <iostream>
#include <complex>
int main ()
{
std::complex<double> z1 (1,2);
std::cout << "real part: " << std::real(z1) << 'n';
std::cout << "imag part: " << std::imag(z1) << 'n';
return 0;
}
结果:
real part: 1
imag part: 2
abs函数
复数的模也就是向量的长度,它可以根据复数的实部与虚部数值的平方和的平方根的值求出。我们常利用abs函数计算信号的幅度大小。
![]()
complex头文件中取模函数是abs,其定义:
template<class T> T abs (const complex<T>& x);
示例:
#include <iostream>
#include <complex>
int main ()
{
std::complex<double> z1 (3.0,4.0);
std::cout << "Absolute value: "<< std::abs(z1) << std::endl;
return 0;
}
结果:
Absolute value: 5
conj函数
在上面的除法运算中,我们知道,如果实部相同,虚部互为相反数,那么它们互为共轭复数。complex也提供了一个函数conj便于我们求解一个复数的共轭复数。
template<class T> complex<T> conj (const complex<T>& x);
示例:
#include <iostream>
#include <complex>
int main ()
{
std::complex<double> z1 (2.0,3.0);
std::cout << "z1: " << z1 << std::endl;
std::cout << "z1 conjugate: " << std::conj(z1) << std::endl;
return 0;
}
结果:
z1: (2,3)
z1 conjugate: (2,-3)
arg函数与polar函数
arg和polar是两个”相反“的函数,这两个函数可以进行相互转换。arg函数作用是根据一个复数返回一个角度,而polar函数可以根据角度返回一个复数。它们在计算相位或者根据相位计算其对应的IQ时较为常用。
template<class T> T arg (const complex<T>& x);
template<class T> complex<T> polar (const T& rho, const T& theta = 0);
示例:
#include <iostream>
#include <complex>
int main ()
{
std::complex<double> z1 (3,4);
double theta = std::arg(z1);
std::complex<double> z2 = std::polar(5.0, theta);
std::cout << "angle:" << theta << std::endl;
std::cout << "polar:" << z2 << std::endl;
return 0;
}
上面的示例先用arg函数求出对应的theta角,然后,再用polar函数根据求出的theta角以及幅值r返回相应的复数,结果如下:
angle:0.927295
polar:(3,4)
norm函数
norm函数可以计算复数的平方和,即实部和虚部平方的和,可用于计算IQ数据的功率大小。其定义如下:
template<class T> T norm (const complex<T>& x);
示例:
#include <iostream>
#include <complex>
int main ()
{
std::complex<double> z1 (3.0,4.0);
std::cout << "z1 norm: " << std::norm(z1) << std::endl;
return 0;
}
结果:
z1 norm: 25
exp函数
complex也支持自然指数,我们可以使用exp函数。通过这个函数,我们就可以生成我们想要的复指数信号了。
template<class T> complex<T> exp (const complex<T>& x);
我们可以利用这个函数生成一个theta角为pi的复指数数据,示例代码:
#include <complex>
#include <iostream>
int main()
{
double pi = std::acos(-1);
std::complex<double> i(0, 1);
std::cout << std::fixed << " exp(i*pi) = " << std::exp(i * pi) << 'n';
}
运行结果如下:
exp(i*pi) = (-1.000000,0.000000)
最后
毋庸置疑,复数的提出对数学界来说是一个全新的发展,复数扩展了数的概念,让数从一维变成了二维。复数也是现代数字通信行业发展的必要条件,它是数字信号处理的基础。数字信号处理是一个极为抽象和复杂的学科,掌握复数的处理方法对数字信号处理应用实为必要,因此大家一定要熟练掌握这些方法的应用。
 芯耀
芯耀




 3403
3403

 下载ECAD模型
下载ECAD模型






