谈谈欧拉公式与复指数信号

在之前的发文中，欧拉公式推导过程中有一处笔误，将sin(x)和cos(x)的泰勒展开式颠倒，本次更新特别进行更正。在此，特别鸣谢"不逃避，不回头，不后退！"这位粉丝朋友。

正文：

在无线通信中信息的传递是通过电磁波的形式传递出去的。电磁波可以用一系列不同频率的正弦函数来表示，我们可以利用正弦信号的幅度、频率、相位这三个特性进行信号的调制。在进行信号处理时，如果使用正弦信号进行分析，就需要进行复杂的三角函数运算，计算会相当的繁琐。

不过，一个大牛早就帮我们找到了一个新的方向。他就是瑞士的数学家和物理学家——莱昂哈德.欧拉，他提出了一个可以说是世界上最完美的公式——欧拉公式，在这个公式中将三角函数和复指数完美的关联到一起。于是，我们就可以使用复指数信号进行信号分析，对于复指数来说，其运算比较简洁，我们通常会使用复指数来替代正弦信号进行运算。

废话不多说，直接上公式！

e是自然数；

i是虚数，在通信里我们常用j表示；

cos是余弦函数；

sin是正弦函数；

x是以弧度单位的变量；

欧拉公式的推导

对于公式推导是最让人头疼的，但是不要怕，大家暂时只要做个了解就好，因为在实际应用中也不会让来我们推导这个公式，我们只要记住这个公式即可。下面我们看看欧拉公式的推导过程。

在欧拉公式推导需要用到泰勒级数，先让我们看一下泰勒级数。

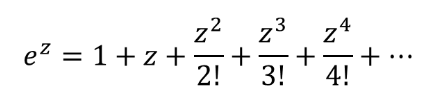
公式中的变量z可以用ix带入，得到表达式（1）：

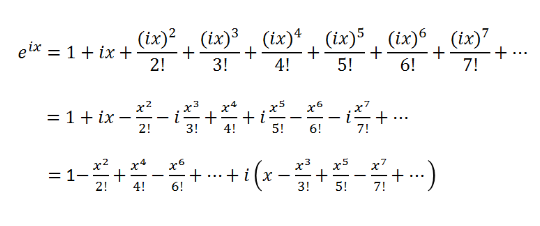
因为sinx和cosx的泰勒展开式，如下表达式（2）和（3）：

所以，最后将表达式（2）和表达式（3）带入到表达式（1），即可得到欧拉公式。

几何意义

因为欧拉公式右边cosθ + i sinθ是一个复数，我们可以将它在复数坐标系上表示，因此，e^(iθ)就是单位圆上的点，实部是cosθ，虚部是sinθ，对应的是从原点到A，辐角为θ，长度为1的单位向量。

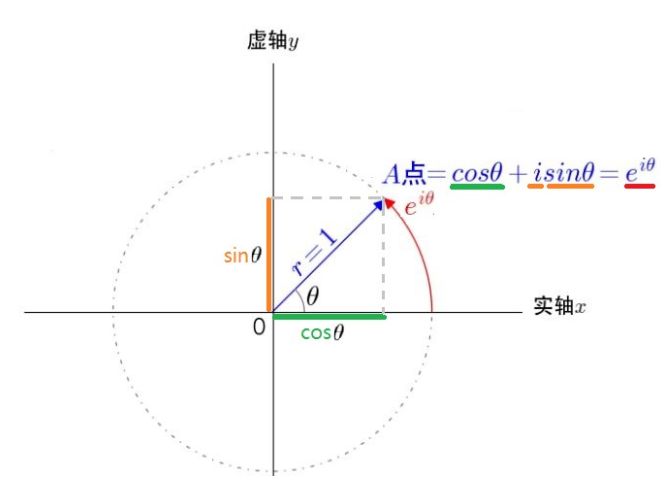
关于虚数i我们该怎么理解呢？

我们先来看看复数和复指数相乘会是什么情况？例如，复数z=r(cos(φ) + isin(φ))。

根据欧拉公式，可知：

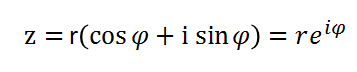
复数z和复指数e^(iθ)相乘：

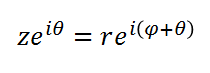
我们看到当复指数乘以复数，相当于这个复数对应的向量旋转θ，θ大于0逆时针旋转，小于0则顺时针旋转。

现在我们来看看复数i，我们将它换一种形式表示。当θ=π/2时，i=cos(π/2) + i sin(π/2)，再根据欧拉公式得：

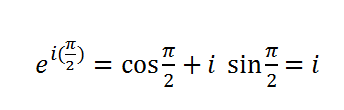
所以复数与i相乘，就相当于复数对应的向量逆时针旋转90度。

复指数信号

对于复指数信号，我们可以再引入一个时间变量t，θ随着时间t以角速度ω变化，即θ=ωt+φ。因此，复指数信号可以表示为：

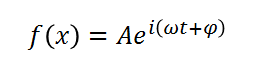
根据ω = 2πf，也可表示为：

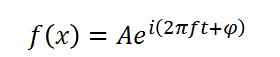
A；幅度；

ω：角速度；

f：频率；

φ：初相；

复指数信号是什么样的呢？下面的图形就是复指数信号的运动轨迹，它的运动轨迹是螺旋前进的三维图形，从图中可以看出，复指数信号在复平面上的投影是个圆，在实轴和虚轴上的投影分别是余弦和正弦函数。

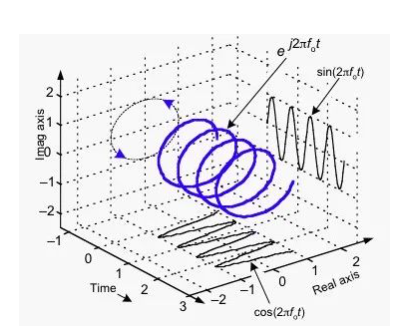
其实，复指数信号并不简单，但是其运算的简洁性，恰恰为复杂的信号处理运算提供了简洁的数学工具。