如何理解相位？

“人有悲欢离合，月有阴晴圆缺”。这是我们在中学时期学的东坡先生在《水调歌头》里的非常有名的一句词，这里的阴晴圆缺指的就是月相的变化。那么，我们该怎么描述信号的相位的呢？

在学习相位之前，我们先来了解一下什么叫相，就以月相举例来说，因为太阳，地球，月亮三者在运动的过程中相对位置会发生变化，我们在地球上看到月亮反射太阳光的形状也会不同。通常我们把我们在地球上看到的形状叫做月相。

由于月球是围绕地球公转，他们的位置会是周期性变化的，月相也是周期性变化的，每一种形状对应一个月相。

上面我们知道了什么是月亮的月相，那么，什么是月亮的相位呢？古人真的是聪明呀，他们根据月相的周期性变化规律发明了月历。这里的月历我们可以理解为月亮的相位。比如，我们俗语里说的“十五的月亮十六圆”，这里的十五和十六其实就是月亮的相位。十五或十六日时月相是满月，十五或十六代表了月相已经从新月开始变化到满月状态，是完整周期30天的一半左右的位置，我们可以用月历来度量这种位置关系。

看了上面的月亮的例子，大家应该对相和相位有个初步的了解吧。这里我们可以简单总结一下：

相：它是一种在某种循环周期变化里的一个状态。月亮的每一种月相反映的是一种我们看到的月亮的形状。

相位：它是从某一个参考点开始测量到另外一个点的状态变化的度量值，对应于周期变化的位置关系。这里就好理解了我们说月历就是代表相位了。

接下来我们再来看下在通信里相和相位又是什么？

以一个正弦波为例，它是一个周期变化的信号，通过他的波形我们可以看出。在每个周期里它的变化规律都是从幅度为0开始逐渐变大到最大值（正），然后，开始减小到0，再继续减小到最小值（负），最后，又开始增大到0，然后，进入下一个周期……

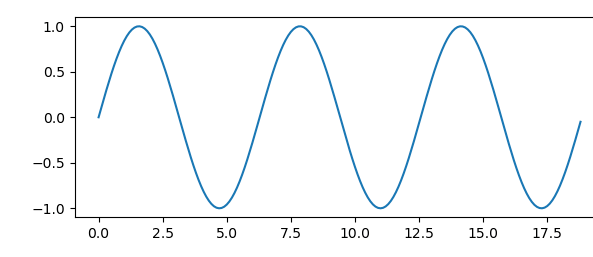
这里的最大值和最小值我们称做波峰和波谷。对于波峰来说，这时它的值最大，处在值将要变小的状态；对于波谷来说，它的值最小，处在值将要变大的状态。这种状态其实就是代表正弦波的相。而对于波峰和波谷这两点他们在变化中对应的位置关系，我们可以用相位来描述。下面我们通过向量的形式，进一步来理解相位。

在之前的复指数信号的篇章《谈谈欧拉公式与复指数信号》中我们知道在复指数的运动轨迹在复平面上是一个向量做圆周运动，在虚轴上的投影是一个正弦函数。

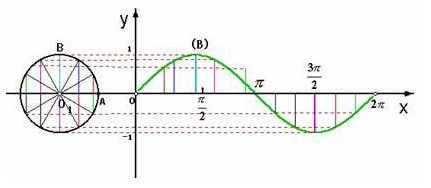
假如这里向量旋转的角速度为ω，那么，它的相位可以用θ = ωt来表示。我们可以看出，相位实际上是一个角度，对应的是向量旋转的角度。在这里就可以理解为什么上面说波峰或者波谷的位置关系可以用相位描述了。从上面旋转向量上来看，以第一个周期为例，在波峰和波谷位置对应向量旋转了π/2 和3π/2，所以对应的相位就是π/2 和3π/2。

我们再思考这样一个问题，对于周期变化的正弦信号来说，会存在很多个波峰和波谷或者其他的值，那么，我们如何确认对应的是哪个周期的点呢？答案是显而易见的，我们可以通过相位确定这种关系。

通常，我们需要把初始相位φ考虑进去，那么，相位的计算公式就是θ=ωt+φ。

最后，需要注意到是相位实际上发生在有周期变化规律的场景下，它是信号状态变化的度量，对应的是周期运动的位置关系，这个度量我们可以用角度表示，我们也可以称为“相角”。