7025
在之前的文章《一文讲透超宽带（UWB）前世今生》中，我们从起源、定义、标准、发展、应用等角度概述了UWB技术。根据UWB的特性，其基础功能分为：数据传输、雷达成像、测距定位。接下来我们将概述其数据传输和雷达成像功能，并对UWB当前的主要运用：测距定位功能进行深入解析。
►►►数据传输功能概述
► UWB具有天然的安全性，由于UWB信号一般把信号能量弥散在极宽的频带范围内，对于一般通信系统来说，UWB信号相当于白噪声信号，从电子噪声中将脉冲信号检测出来是一件非常困难的事。
► UWB的射频部分采用随机编码对UWB脉冲信号进行伪随机化后，脉冲监听将更加困难。
► 实际应用中，CCC联盟与802.15.4工作组提出在UWB的PHY层和数据链路层中，在每一帧的发送中，都对整体数据与时间戳加密（防篡改时间戳），这样使UWB通信有了极高的安全性。
图2 UWB数据传输
1.2UWB数据传输应用
UWB的标准中主要定义了相关的物理层与链路层，所以并没有一个类似于蓝牙的协议栈，因此用户可以直接将自己的数据向信道中发送，如苹果所使用的U1芯片，采用的UWB的协议就是苹果自行定义的私有协议，对于任何一个UWB的组织用户都可以使用自己的通讯协议进行数据的交流。
图3 UWB在802.15.4中定义的MAC层通用帧格式
►►►雷达成像功能概述
UWB利用超短脉冲信号，通过测量信号的时延和幅度来确定目标的位置和速度。因此，UWB可用作雷达成像。UWB雷达的超宽带信号带宽非常宽，可以达到几个GHz。这种信号具有很短的脉冲宽度和很高的峰值功率，可以穿透障碍物并在复杂环境中进行探测。
UWB雷达发射脉冲信号，并接收该脉冲信号经障碍物反射后的回波，通过对回波扰动的分析来判断UWB雷达附近是否存在物体，这种检测方式我们称之为CIR（Channel Impulse Response，信道脉冲响应）技术。UWB雷达通过接收到的CIR来探测周围物体及其运动。当UWB雷达周围有物体时，CIR对应位置就会有脉冲峰；当周围物体运动时，由于多普勒效应，对应的CIR值就会变化。通过分析CIR频谱来估计目标运动状态。
2.2UWB成像原理
UWB成像技术是UWB雷达的扩展应用，UWB成像可以简单理解为UWB脉冲波组成一堵无形的墙，这面墙向前走的时候碰到任何物体都会局部反弹回去，这面初始平整的墙返回的时候就有了凹凸变化，这个凹凸变化就描绘出了物体的一个面。
UWB成像通过软件算法解析实现，对于UWB硬件底层，只需要将检测的这一个区域变化的曲线，如上图的一个整体趋势告知算法，用算法的运算来描绘出物体的样貌，这种成像的方式是应用层所关注且通用的，除UWB雷达外，底层硬件不管使用毫米波雷达还是激光雷达，其成像原理都是采用的这种方式。
2.3UWB雷达成像应用
当前UWB雷达成像应用最广泛的领域主要包括：
► 军事领域：便携式UWB穿墙雷达能够实现对障碍物后面目标的探测、定位、成像和追踪。在应用层面主要包含建筑内部成像，探测、跟踪运动目标。在军事装备、火灾及地震救援等场景有着广泛的应用前景和价值。
► 医疗领域：非接触式UWB生命监测雷达不同于传统的电极和传感器接触的检测形式，可实现较远距离无接触式检测患者的呼吸和心跳，可以在不影响患者正常休息的情况下，实现对患者的生命体征实时监测。
► 车载领域：UWB活体雷达通过活体微动作感知算法，实现车内生命体征的非接触式存在性检测，支持静态呼吸检测，有效防止儿童、宠物等无行为能力的乘客滞留车内。UWB脚踢雷达基于运动感知算法，实现车尾箱的非接触式脚踢检测。
►►►测距定位功能解析
► 双向测距(TWR，Two Way Ranging)
双向测距顾名思义就是通过两边的一收一发以及一发一收的相互配合下进行的测距，与比较常见的红外测距不同，红外测距就是典型的单向测距即为只用一个设备，发和收获取到了位置，缺点也很明显，必须有一个合适的反射点，双向测距则解决了这个问题，双方进行通讯后获取到了距离信息，且是双方都可以获取到测距信息。
► 单边双向测距(SS-TWR，Single Side-TWR)
前文讲解了测距的基本物理原理，这里我们就来讲解一下UWB测距的最基础的实现原理，单边双向测距。
SS-TWR原理，如下图，Device A在其自己时钟TA1 时刻发起测距，Device B在其自己时钟TB1时刻收到了Device A发起的测距帧，即Tprop1 = (TB1-TA1 ) Device A 于Device B的距离就应该是Tprop *C(光速)。但是由于Device A 和Device B 时钟不同步，所以无法确认Tprop1 的值。为了确定Tprop1 的值，Device B在收到Device A发起的测距帧后，固定延时Treply 的时间回复Device A,发射时间为TB2, Device A在TA2的时刻收到，即Tprop2 = (TA2-TB2)，假设在这段时间，Device A设备Device B的位置没有发生过改变。那么理论Tprop1 = Tprop2。为了确认Tprop的时间，在Device A的时间轴上，从发送时刻TA1 到收到Device B 回复帧的时刻TA2的耗时Troud = (TA2-TA1 )，在Device B的时间轴上，收到Device A 发起测距帧的时刻TB1到自己回复Device A 的时刻TB2的耗时Treply = (TB2-TB1 )。所以Tprop = (Troud - Treply)/2。即距离为Tprop *C。
图6 SS-TWR测距原理
举个例子：
地球和火星的距离。来自地球的老王，打电话给在火星上的老马并看了现在的时间12:00:00(时分秒)，老马接到电话，时间是18:00:00，过了一会儿，在18:05:00老马打了电话给老王，老王在12:13:00接到电话。因为他们的频率是一致都是以秒为单位(假设)，通过这些数据可以计算信号在地球和火星间飞行的时间，往返的时间是13-5=8分钟，(8分钟/2)*C(光速)即为地球距离火星的距离。
► 双边双向测距(DS-TWR，Double Side - TWR)
其实双边测距是从单边测距扩展而来，主要是用于解决测距双方时钟精度不一致导致的误差问题。
在SS-TWR的基础上，由于设备自身时钟，由于温度以及设备精度误差等原因导致的时钟偏移，即Treply延时时间越长，从而导致计算距离时的误差越大。为了减小以及消除这种误差，DS-TWR增加反向测量补偿，如下图所示。使用两个往返时间测量，降低Treply的延时带来的误差。
即
距离为Tprop *C。
图7 DS-TWR测距原理
3.2基于测距的定位方式（三边定位）
► 基于测距的定位原理
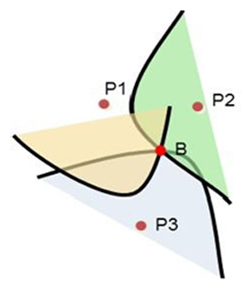
我们已经获知了距离，如果我们想进一步知道这个待定位对象（未知点）在这个空间的哪个地方或者在这个二维平面的哪个坐标点，就需要定位解算，从距离转化为坐标点必须有三个已知点以及待定位对象（未知点）与这三点之间的距离，拿到这些数据后即可获知待定位对象（未知点）的坐标点。基于测距的定位原理，其实从数学的角度分析，抽象后只有一种，就是毕达哥拉斯定理（Pythagorean Theorem）。这位古希腊数学家用代数的方式来描述平面几何，毕达哥拉斯定理其实在中国有一个更广为人知的名字即“勾股定理”。
► 三边定位解算
对于距离推算坐标，最简单的方式就是画圆，在理想情况下（三个圆均相交），三个圆会相交于一点，公式如下：
已知三点位置 (x1, y1), (x2, y2), (x3, y3)
已知未知点 (x0, y0) 到三点距离 d1, d2, d3
以 d1, d2, d3 为半径作三个圆，根据毕达哥拉斯定理，得出交点即未知点的位置计算公式：
但是对于距离计算，是不存在绝对理想的情况的，很大概率是三个圆相交甚至相离的情况下，计算出估计出一个近似值。
图8 三角定位原理
当 z = 0 时， 即为三个圆在水平面上相交为一点，首先解出 x:
将公式二变形，将公式一的 z^2 代入公式二，再代入公式三得到 y 的计算公式：
当然以上只是一个基本的公式推导，有助于大家进行理解，但是实际使用时我们不可能去不断进行坐标的转化然后解算，这样的处理过于浪费时间，代码也是很难实现。这时我们只需要引入线性代数将矩阵运算带入其中就可以简单快速的得到通用解答式。
基本公式组保持不变
进行拆解销项
经过线性代数矩阵的分割后
若我们令
为A矩阵
为B矩阵
那么待求未知点坐标（X,Y）为
3.3基于到达时间差的定位方式(TDOA)
► TDOA
TDOA（Time Difference Of Arrival，到达时间差），是基于各参考基站（以下简称Anc）与待定位对象（以下简称Tag）之间的距离之差通过求解非线性双曲方程组来推断待定位对象相对于各参考基站的相对位置的定位方法。当基站之间的时间是完全同步的情况下，且晶振在一段时间内的误差极小（ppm的值极小），那么时间差值就是距离差值，原因是电磁波的传播速度是固定的。当Tag端发射一个信号到达几个Anc端后，只需要测量Tag发出的信号到达各Anc的到达时间之差即可得到对应的距离之差。
► 双曲定位解算
使用TDOA的前提就是各个基站有一个很精准的时间同步，这样才能保证Tag端发送出来的时间到达各个基站后有一个很高精度的时间差值。那么时间差值又如何转化为距离差值后又转化为坐标点呢？如果说测距后的三边定位是来解三个圆的相切问题，那么TDOA就是来解非线性双曲方程组。在TDOA定位系统中，进行定位解算时，首先需要根据到达时间差建立双曲线方程组：
Tag坐标：(X,Y)
各Anc坐标：(Xi,Xi),i = 1,2,3
各Anc到Tag的距离记为：
各Anc与A1到Tag的距离差记为：
那么这时候方程组的建立如下
求解非线性方程组的第一步通常都是要做线性化处理。
一种常见的线性化处理是进行泰勒级数展开并保留前两项，这里就不详细展开说明了，整体求解的图示如下：
图9 双曲定位原理
AOA（Angle of Arrival，到达角度测距），是基于信号到达角度的定位算法是一种典型的基于测距的定位算法，通过某些硬件设备感知发射节点信号的到达方向，计算接收节点与锚节点之间的相对方位或角度，然后再利用三角测量法或其他方式计算出未知节点的位置。
► PDOA
PDOA（Phase Diference of Arrival，信号到达相位差），是通过测量相位差求出信号往返的传播时间来计算往返距离。本质上PDOA是AOA定位算法的一种延申。
► 相位差定位解算
其中α代表两根天线接收的信号中的First-Path 的到达相位之差（Phase Difference of Arrival），这也是PDOA 名字的来由。
图10 相位差定位原理
下载ECAD模型
