今天给大侠带来基于FPGA的扩频系统设计,由于篇幅较长,分三篇。今天带来第一篇,下篇。话不多说,上货。
在无线通信系统中,普遍使用扩频通信技术,因此扩频技术对通信系统具有重要的现实意义。直接序列扩频技术是应用最广的一种扩频技术,FPGA具备高速度的并行性特点在无线通信系统中的优势日益增强,利用FPGA实现直接序列扩频技术,可增大传输速率,可以使扩频技术有更好的发展与应用。
本篇利用本原多项式产生伪随机序列用作扩频,通过同步模块对扩频后的信号进行捕获,通过直接序列解扩模块进行解扩。本篇给出了编解码、扩频解扩、同步的整体方案,使用Quartus实现功能,并结合Matlab和ModelSim对模块进行调试和测试,实现扩频通信模块的搭建仿真,验证其设计的正确性。首先概述了方案设计与论证、整体方案的设计、各个模块的设计、个别模块的调试与各个模块的仿真验证。本篇主要实现的模块有:汉明编码模块、直接序列扩频模块、量化器模块、同步模块、直接序列解扩模块和汉明译码模块。各位大侠可依据自己的需要进行阅读,参考学习。
第三篇内容摘要:本篇会介绍分析调试,包括汉明码解码模块调试、直接序列扩频模块调试、同步模块调试、整体设计资源占用率、整体设计RTL设计图,还会介绍系统测试,包括汉明编码模块测试、直接序列扩频模块测试、量化器模块测试、同步模块测试、直接序列解扩模块测试、汉明译码模块测试、系统整体测试等相关内容。
四、分析调试
4.1 汉明编解码模块调试
首先利用Matlab该模块进行调试,利用随机函数生成10个随机数,通过74汉明码编码函数对10个随机函数进行编码,随机数分别为4’h0、4’hb、4’h6、4’h1、4’h3、4’h9、4’h7、4’h9、4’h7和4’hd,编码后分别为7’h00、7’h4b、7’h46、7’h51、7’h23、7’h39、7’h17、7’h39、7’h17和7’h0d。具体如图4.1所示,对应Matlab代码详见附录A。
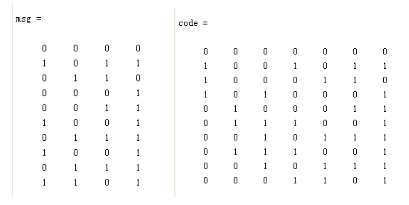
图4.1 汉明码编码Matlab仿真图
利用Matlab的随机函数生成10个随机数,通过74汉明码编码函数对10个随机函数进行编码,编码后引入噪声如图4.2所示:

图4.2 编码后与加入噪声后对比图
通过译码函数进行译码,如下图4.3所示:
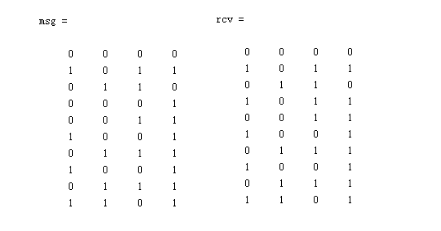
图4.3 编码前与译码后对比图
根据图4.3可知,当发生一位码值错误时,汉明译码模块可以正确纠错;当发生一位以上码值错误时,汉明译码模块不能正确纠错,导致译码错误。利用Matlab可知汉明译码模块具有译码能力和一位码值的纠错能力。
利用Verilog对汉明码编码模块和汉明译码模块进行编写,然后一同进行调试,在两个模块中间加一噪声模块,保证编码后数据任意一位发生错误,通过译码模块后,判断是否能够进行正确纠错,编码前数据与编码后的数据是否一致,判断两个模块的正确性,调试模型如图4.4所示:
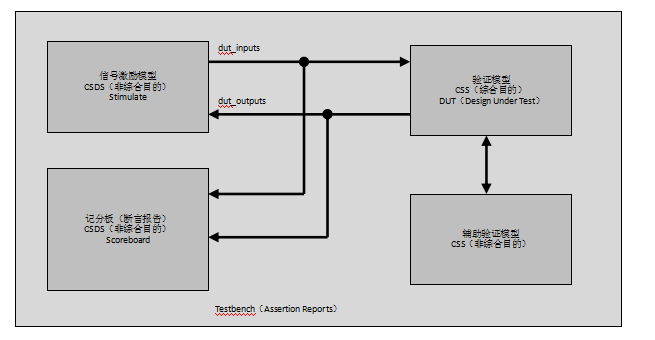
图4.4 断言调试模型
ModelSim仿真波形截图如图4.5所示:

图4.5 汉明编解码模块仿真波形图
利用断言的仿真方式打印报告如图4.6所示,通过确认编解码前后数据一致,也证明汉明编码模块和汉明译码模块正确性。
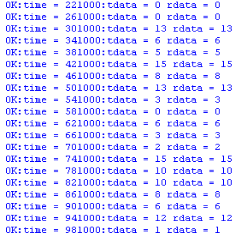
图4.6 打印结果图
4.2 直接序列扩频模块调试
利用Matlab对该模块进行调试,利用Matlab伪随机函数生成伪随机数,通过设置初始值来与3.4.2节表3.2的结果进行对比,通过对比可以确定生成伪随机序列满足要求,为采用Verilog设计打好坚实的基础。如图4.7为Matlab生成的伪随机数,对应Matlab代码详见附录A。

图4.7 Matlab生成伪随机数图
4.3 同步模块调试
在进行同步调试时出现对不齐同步头的问题,例如计算所延时时间应为29个系统时钟周期,即计数器仅需要延时29个时钟周期,因为计数器是从“0”开始进行计数,当计数值等于延时时间-1时,模块可以进行同步头解扩处理,由于没有对齐同步头,导致利用最小二乘法计算结果均大于预设阈值,系统无法进行下去。仿真波形截图如图4.8所示:
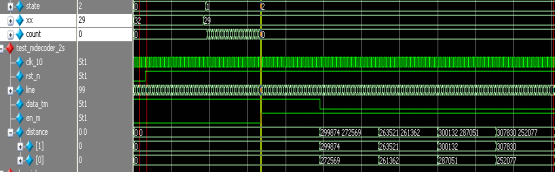
图4.8 同步错误情况仿真波形图
根据仿真波形结合设计代码最终找到原因,由于同步模块对延时时间信号进行捕获也需要一个系统时钟周期,所以计数器的计数值应该等于延时时间-2,模块才可以进行同步头解扩处理,仿真波形截图如图4.9所示:
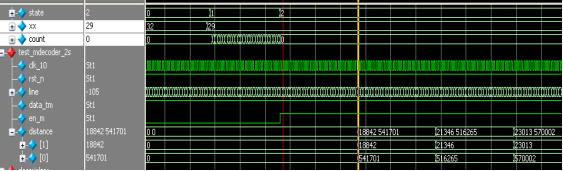
图4.9 同步修改正确仿真波形图
4.4 整体设计资源占用率
在设计完成后,在如图4.10所示,该整体设计共使用3735个组合逻辑,占5%;使用1782个寄存器,占3%;使用39个I/O引脚,占6%;使用5888个存储器,约占1%;使用2个9bit嵌入式硬件乘法器,约占1%。

图4.10 FPGA资源占用率
4.5 整体设计RTL视图
由于例化的原因导致与整体设计框图不一致,因为例化对其整体设计功能无影响。所以设计整体RTL视图如图4.11所示:
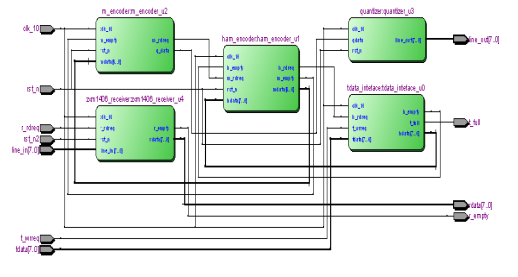
图4.11 设计整体RTL图
五、系统测试
对整体系统设计进行测试,通过发送端到接收端的各个模块逐级进行测试,确保每个环节的正确性。
5.1 汉明编码模块模块测试
利用Verilog进行汉明码编码模块进行编写。在testbench测试文件总输入数据初始化为8’h55,通过时钟上升沿到来进行取反,所以数据依次为8’h55、8’haa、8’h55…8’haa等,接口采用同步fifo进行数据缓冲,如图5.1所示,在测试文件中通过判断t_full信号高有效来判断fifo是否为满状态,若不是满状态,则置写操作的使能信号t_wrreq高电平有效,对fifo进行写操作,否则不进行写操作。汉明码编码模块通过判断h_empty信号来判断fifo是否为空状态,若不为空,则置读操作使能信号h_rdreq高电平有效对fifo进行读操作,否则不进行读操作。
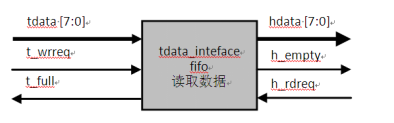
图5.1 fifo接口图
通过汉明码编码模块对数据进行汉明码编码,如图5.2所示,信号ha_data为对应编码结果。4’h5编码为7’h2d,4’ha编码为7’h52,如图5.2表明,汉明编码模块能够正确编码。
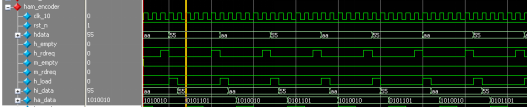
图5.2 汉明码编码模块ModelSim仿真波形图
5.2 直接序列扩频模块测试
利用Verilog进行伪随机数模块编写,初始值为5’b00001,生成序列为如图5.3所示。信号m_bit为伪随机数,在进行编码数据信号进行扩频之前,应将数据信息加上帧头14’b11111111111110,信号m_data为汉明编码模块编码后的7bits数据信息,信号s_bit为帧头或编码数据信息并串转换后的信号,信号bc控制信号s_bit哪个数据位于信号m_bit相异或,得到的结果为输出信号q_data,从而实现直接序列扩频的功能。如图5.3表明,直接序列扩频模块能够正确完成扩频。
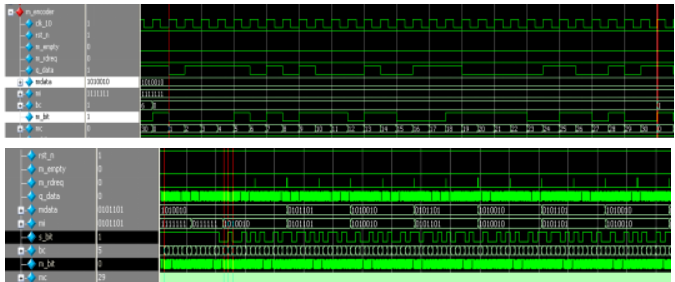
图5.3 直接序列扩频模块ModelSim仿真波形图
5.3 量化器模块测试
量化器模块将单比特的信号变为8bits有符号数,仿真波形截图如图5.4所示,可以确定量化器模块能够正确进行对信号量化。

图5.4 量化器模块ModelSim仿真波形图
5.4 同步模块测试
为了模拟实际传输过程,扩频信号再进入同步模块前引入±46的噪声,实际输入值信号line如图5.5所示:

图5.5 加入噪声后ModelSim仿真波形图
利用最小二乘法对输入信号与31个模板进行计算,得到小于阈值的唯一的延时数据信号xx如图5.6所示,模板2满足要求,信号xx计算值为29,因此要进行29拍解扩时钟周期的延时,来对齐同步头。
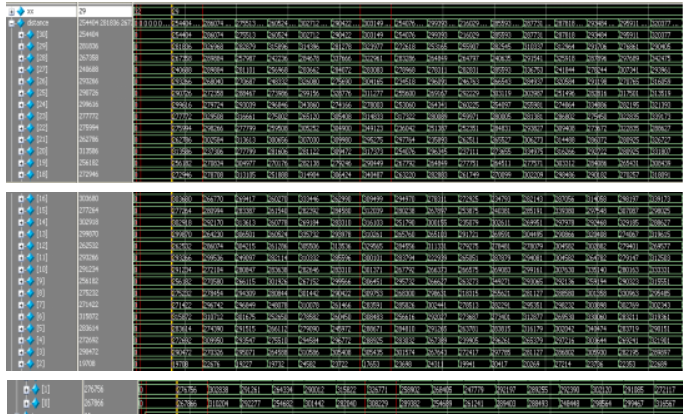
图5.6 计算延时ModelSim仿真波形图
通过延时达到对齐同步头的目的,对齐使能信号en_m为高电平,说明已对齐。如图5.7所示:

图5.7 同步头对齐ModelSim仿真波形图
对齐后将数据信号每31bits与模板“0”模板“1”进行最小二乘法计算,如图5.8所示:

图5.8 同步头解扩ModelSim仿真波形图
信号data_tm为判断出的信号数据,当检测到同步头最后一位的“0”数据信息后,说明同步头已结束,同步功能已实现。如图5.9所示,同步模块能够正确实现同步。
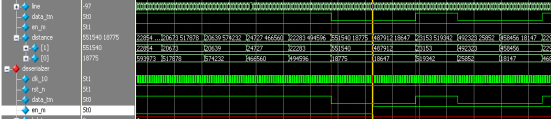
图5.9 同步头识别ModelSim仿真波形图
5.5 直接序列解扩模块测试
当检测到最后一位为“0”后,进入数据信号解扩过程,与同步头解扩相类似,只是把解扩后的数据利用计数器的计数值,写到寄存器对应的位置,同时进行串并转换功能,信号bc为计数器,信号hdata_reg1为串并转换后存储数据的寄存器。如图5.10所示,直接序列解扩模块能够正确实现解扩。
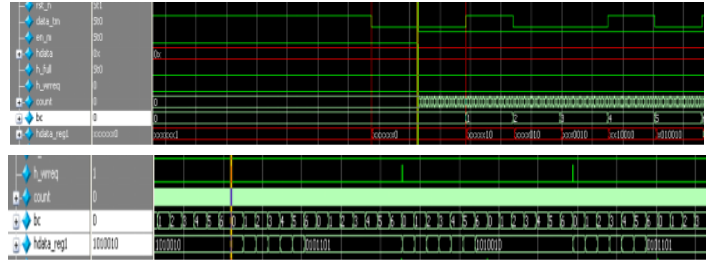
图5.10 数据信息解扩ModelSim仿真波形图
5.6 汉明译码模块测试
利用Verilog对汉明译码模块进行编写。通过直接序列解扩模块后的数据经过汉明译码模块后,如图5.11所示:

图5.11 汉明译码ModelSim仿真波形图
信号data_reg被译码正确后通过对fifo的满标志信号H_full高电平进行判断,若为高电平则不进行写操作,若为低电平则将fifo的写使能信号置高进行写操作,将译码后的数据写入fifo中。如图5.12所示,汉明译码模块能够对数据进行正确译码。
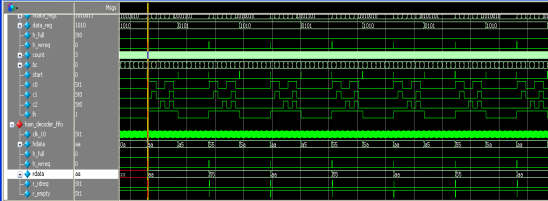
图5.12 数据输出端口仿真截图
5.7 系统整体测试
通过打印信息确认,原始数据与译码后的数据一致,能够确认系统整体设计正确,如图5.13所示:
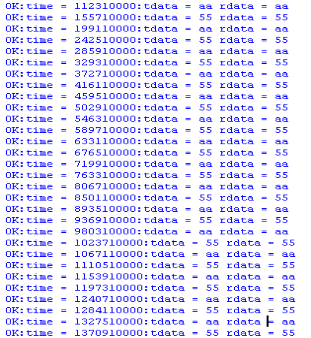
图5.13 打印结果截图
引用2.1节设计要求,总结系统整体设计完成对应功能情况,如表5.1所示:
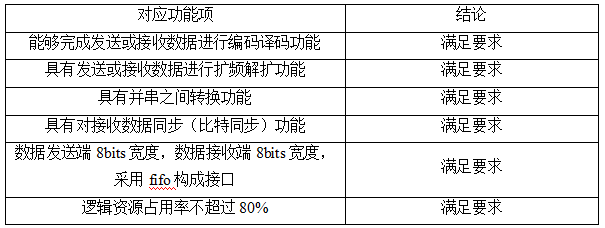
表5.1 系统功能测试表
结 论
直接序列扩频是主流的扩频通信之一,有着许多重要特点与优点,本篇利用FPGA的处理速度和并行运行等特点,设计完成了一个基于FPGA扩频模块设计。在利用Quartus II、Matlab和ModelSim对直接序列扩频模块进行了仿真分析。利用伪随机序列进行扩频,是扩频模块获得高抗噪声性能和抗干扰性能的关键。
本文首先对直接序列扩频模块一般原理进行介绍,然后重点分析直接序列扩频解扩,合理分配功能模块、准确掌握各个模块之间的控制和被控制的关系,以及整体时序关系。通过从接口fifo读取数据后,采用汉明编码模块,完成了对数据的编码,在完成编码后加入同步头,为同步做准备。利用本原多项式产生伪随机数,伪随机数与编码后的数据进行异或处理,已达到扩频的目的,扩频后的数据进行量化且引入噪声送入同步模块。同步模块利用31个伪随机数的模板,采用最小二乘法对数据进行计算,计算值小于预定阈值,则该数据对应的信息为接收端需要进行延拍的个数,对齐后利用2个伪随机数的模板对数据进行“0”和“1”的判断,当同步头数据值出现“0”后,代表下一位开始为数据信息,直接序列解扩模块开始进行解扩处理,和同步模块同理,将数据与2个伪随机进行最小二乘法的计算,从而达到解扩的目的。解扩后的数据通过汉明译码模块进行译码后写入接口fifo,再通过fifo输出。经过验证该整体模块达到扩频的目的,提高了抗噪声的能力,各个模块能够正确完成对应功能。
附录部分源代码
伪随机数Matlab代码:
polynomial=[1 0 0 1 0 1];
reg=[0 0 0 0 1];
grade=length(polynomial)-1;
PN_Length=(2^grade-1);
pn=zeros(1,PN_Length);
n=0; c=zeros(1,grade);
for i=grade:-1:1
if polynomial(i)==1
n=n+1;
c(n)=grade+1-i;
end
end
q=0;
for i=1:PN_Length
p(i)=reg(1)
m=reg(grade+1-c(1));
for q=2:grade
if (c(q)>0) & (reg(grade+1-c(q))==1)
m=~m;
end
end
for q=1:(grade-1)
reg(q)=reg(q+1);
end
reg(5)=m;
end
汉明码编码译码Matlab代码:
k=4;
n=7;
msg=randint(10,4,2)
code=encode(msg,n,k)
code_noise=rem(code+rand(10,7)>0.95,2)
rcv=decode(code_noise,n,k)
disp(['Error rate in the received code:' num2str(symerr(code,code_noise)/length(code))])
disp(['Error rate after decode:' num2str(symerr(msg,rcv)/length(msg))])
汉明码编码Verilog代码:
module hamming74(clk_10, rst_n, hi_data, ha_data, hm_sel);
input clk_10;
input rst_n;
input [7:0] hi_data;
output reg [6:0] ha_data;
input hm_sel;
wire [3:0] hm_data;
wire q0,q1,q2;
assign hm_data = hm_sel ? hi_data[7:4] : hi_data[3:0];
always @ (posedge clk_10)
begin
if(!rst_n)
begin
ha_data <= 0;
end
else
begin
ha_data[6] <= hm_data[3];
ha_data[5] <= hm_data[2];
ha_data[4] <= hm_data[1];
ha_data[3] <= q2;
ha_data[2] <= hm_data[0];
ha_data[1] <= q1;
ha_data[0] <= q0;
end
end
assign q0 = hm_data[0] ^ hm_data[1] ^ hm_data[3];
assign q1 = hm_data[0] ^ hm_data[2] ^ hm_data[3];
assign q2 = hm_data[1] ^ hm_data[2] ^ hm_data[3];
endmodule
伪随机数产生Verilog代码:
module m_generator(clk_10, rst_n, m_bit);
input clk_10;
input rst_n;
output m_bit;
reg [4:0] q;
parameter KEY = 5'b00001;
always @ (posedge clk_10)
begin
if(!rst_n)
begin
q <= KEY;
// q <= 0;
end
else begin
q[0] <= q[1];
q[1] <= q[2];
q[2] <= q[3];
q[3] <= q[4];
q[4] <= q[3] ^ q[0];
end
end
assign m_bit = q[0];
endmodule
伪随机序列与数据信息异或处理Verilog代码:
module me_xor(clk, rst_n, s_bit, m_bit, q_data);
input clk, rst_n;
input s_bit, m_bit;
output reg q_data;
always @ (posedge clk)
begin
if (!rst_n)
q_data <= 0;
else
q_data <= s_bit ^ m_bit;
end
endmodule
量化器模块Verilog代码:
module quantizer(clk, rst_n, qdata, line_out);
input clk, rst_n;
input qdata;
output reg signed [7:0] line_out;
always @ (posedge clk)
begin
if (!rst_n)
line_out <= 0;
else
if (qdata)
line_out <= 63;
else
line_out <= -64;
end
endmodule
最小二乘法Verilog代码:
module m_leastsquare(clk_10, rst_n, line, distance);
input clk_10, rst_n;
input signed [7:0] line;
output reg signed [21:0] distance;
parameter KEY = 5'b00001;
wire m;
reg [4:0] count;
reg signed [21:0] int_distance;
always @ (posedge clk_10)
begin
if (!rst_n || count >= 5'd30)
count <= 0;
else
count <= count + 5'd1;
end
m_generator #(.KEY(KEY)) u_mg(.clk_10(clk_10), .rst_n(rst_n), .m_bit(m));
always @ (posedge clk_10)
begin
if (!rst_n)
begin
int_distance <= 0;
distance <= 0;
end
else
if (count < 5'd30)
if (!m)
int_distance <= int_distance + (line - 63) * (line - 63);
else
int_distance <= int_distance + (line + 64) * (line + 64);
else
begin
int_distance <= 0;
if (!m)
distance <= int_distance + (line - 63) * (line - 63);
else
distance <= int_distance + (line + 64) * (line + 64);
end
end
endmodule
同步模块Verilog部分代码:
module test_mdecoder_ls(clk_10, rst_n, line, xx);
input clk_10, rst_n;
input signed [7:0] line;
output reg [5:0] xx;
wire signed [21:0] distance [30:0];
wire [30:0] xx_reg;
integer i;
m_leastsquare #(.KEY(5'h01)) u0(.clk_10(clk_10), .rst_n(rst_n), .line(line), .distance(distance[0]));
m_leastsquare #(.KEY(5'h10)) u1(.clk_10(clk_10), .rst_n(rst_n), .line(line), .distance(distance[1]));
m_leastsquare #(.KEY(5'h08)) u2(.clk_10(clk_10), .rst_n(rst_n), .line(line), .distance(distance[2]));
m_leastsquare #(.KEY(5'h14)) u3(.clk_10(clk_10), .rst_n(rst_n), .line(line), .distance(distance[3]));
m_leastsquare #(.KEY(5'h0A)) u4(.clk_10(clk_10), .rst_n(rst_n), .line(line), .distance(distance[4]));
m_leastsquare #(.KEY(5'h15)) u5(.clk_10(clk_10), .rst_n(rst_n), .line(line), .distance(distance[5]));
m_leastsquare #(.KEY(5'h1A)) u6(.clk_10(clk_10), .rst_n(rst_n), .line(line), .distance(distance[6]));
m_leastsquare #(.KEY(5'h1D)) u7(.clk_10(clk_10), .rst_n(rst_n), .line(line), .distance(distance[7]));
m_leastsquare #(.KEY(5'h0E)) u8(.clk_10(clk_10), .rst_n(rst_n), .line(line), .distance(distance[8]));
m_leastsquare #(.KEY(5'h17)) u9(.clk_10(clk_10), .rst_n(rst_n), .line(line), .distance(distance[9]));
m_leastsquare #(.KEY(5'h1B)) u10(.clk_10(clk_10), .rst_n(rst_n), .line(line), .distance(distance[10]));
m_leastsquare #(.KEY(5'h0D)) u11(.clk_10(clk_10), .rst_n(rst_n), .line(line), .distance(distance[11]));
m_leastsquare #(.KEY(5'h06)) u12(.clk_10(clk_10), .rst_n(rst_n), .line(line), .distance(distance[12]));
m_leastsquare #(.KEY(5'h03)) u13(.clk_10(clk_10), .rst_n(rst_n), .line(line), .distance(distance[13]));
m_leastsquare #(.KEY(5'h11)) u14(.clk_10(clk_10), .rst_n(rst_n), .line(line), .distance(distance[14]));
m_leastsquare #(.KEY(5'h18)) u15(.clk_10(clk_10), .rst_n(rst_n), .line(line), .distance(distance[15]));
m_leastsquare #(.KEY(5'h1C)) u16(.clk_10(clk_10), .rst_n(rst_n), .line(line), .distance(distance[16]));
m_leastsquare #(.KEY(5'h1E)) u17(.clk_10(clk_10), .rst_n(rst_n), .line(line), .distance(distance[17]));
m_leastsquare #(.KEY(5'h1F)) u18(.clk_10(clk_10), .rst_n(rst_n), .line(line), .distance(distance[18]));
m_leastsquare #(.KEY(5'h0F)) u19(.clk_10(clk_10), .rst_n(rst_n), .line(line), .distance(distance[19]));
m_leastsquare #(.KEY(5'h07)) u20(.clk_10(clk_10), .rst_n(rst_n), .line(line), .distance(distance[20]));
m_leastsquare #(.KEY(5'h13)) u21(.clk_10(clk_10), .rst_n(rst_n), .line(line), .distance(distance[21]));
m_leastsquare #(.KEY(5'h19)) u22(.clk_10(clk_10), .rst_n(rst_n), .line(line), .distance(distance[22]));
m_leastsquare #(.KEY(5'h0C)) u23(.clk_10(clk_10), .rst_n(rst_n), .line(line), .distance(distance[23]));
m_leastsquare #(.KEY(5'h16)) u24(.clk_10(clk_10), .rst_n(rst_n), .line(line), .distance(distance[24]));
m_leastsquare #(.KEY(5'h0B)) u25(.clk_10(clk_10), .rst_n(rst_n), .line(line), .distance(distance[25]));
m_leastsquare #(.KEY(5'h05)) u26(.clk_10(clk_10), .rst_n(rst_n), .line(line), .distance(distance[26]));
m_leastsquare #(.KEY(5'h12)) u27(.clk_10(clk_10), .rst_n(rst_n), .line(line), .distance(distance[27]));
m_leastsquare #(.KEY(5'h09)) u28(.clk_10(clk_10), .rst_n(rst_n), .line(line), .distance(distance[28]));
m_leastsquare #(.KEY(5'h04)) u29(.clk_10(clk_10), .rst_n(rst_n), .line(line), .distance(distance[29]));
m_leastsquare #(.KEY(5'h02)) u30(.clk_10(clk_10), .rst_n(rst_n), .line(line), .distance(distance[30]));
assign xx_reg[0] = (distance[0]>0 && distance[0]< 19'd50000)? 1'b1:1'b0;
assign xx_reg[1] = (distance[1]>0 && distance[1]< 19'd50000)? 1'b1:1'b0;
assign xx_reg[2] = (distance[2]>0 && distance[2]< 19'd50000)? 1'b1:1'b0;
assign xx_reg[3] = (distance[3]>0 && distance[3]< 19'd50000)? 1'b1:1'b0;
assign xx_reg[4] = (distance[4]>0 && distance[4]< 19'd50000)? 1'b1:1'b0;
assign xx_reg[5] = (distance[5]>0 && distance[5]< 19'd50000)? 1'b1:1'b0;
assign xx_reg[6] = (distance[6]>0 && distance[6]< 19'd50000)? 1'b1:1'b0;
assign xx_reg[7] = (distance[7]>0 && distance[7]< 19'd50000)? 1'b1:1'b0;
assign xx_reg[8] = (distance[8]>0 && distance[8]< 19'd50000)? 1'b1:1'b0;
assign xx_reg[9] = (distance[9]>0 && distance[9]< 19'd50000)? 1'b1:1'b0;
assign xx_reg[10] = (distance[10]>0 && distance[10]< 19'd50000)? 1'b1:1'b0;
assign xx_reg[11] = (distance[11]>0 && distance[11]< 19'd50000)? 1'b1:1'b0;
assign xx_reg[12] = (distance[12]>0 && distance[12]< 19'd50000)? 1'b1:1'b0;
assign xx_reg[13] = (distance[13]>0 && distance[13]< 19'd50000)? 1'b1:1'b0;
assign xx_reg[14] = (distance[14]>0 && distance[14]< 19'd50000)? 1'b1:1'b0;
assign xx_reg[15] = (distance[15]>0 && distance[15]< 19'd50000)? 1'b1:1'b0;
assign xx_reg[16] = (distance[16]>0 && distance[16]< 19'd50000)? 1'b1:1'b0;
assign xx_reg[17] = (distance[17]>0 && distance[17]< 19'd50000)? 1'b1:1'b0;
assign xx_reg[18] = (distance[18]>0 && distance[18]< 19'd50000)? 1'b1:1'b0;
assign xx_reg[19] = (distance[19]>0 && distance[19]< 19'd50000)? 1'b1:1'b0;
assign xx_reg[20] = (distance[20]>0 && distance[20]< 19'd50000)? 1'b1:1'b0;
assign xx_reg[21] = (distance[21]>0 && distance[21]< 19'd50000)? 1'b1:1'b0;
assign xx_reg[22] = (distance[22]>0 && distance[22]< 19'd50000)? 1'b1:1'b0;
assign xx_reg[23] = (distance[23]>0 && distance[23]< 19'd50000)? 1'b1:1'b0;
assign xx_reg[24] = (distance[24]>0 && distance[24]< 19'd50000)? 1'b1:1'b0;
assign xx_reg[25] = (distance[25]>0 && distance[25]< 19'd50000)? 1'b1:1'b0;
assign xx_reg[26] = (distance[26]>0 && distance[26]< 19'd50000)? 1'b1:1'b0;
assign xx_reg[27] = (distance[27]>0 && distance[27]< 19'd50000)? 1'b1:1'b0;
assign xx_reg[28] = (distance[28]>0 && distance[28]< 19'd50000)? 1'b1:1'b0;
assign xx_reg[29] = (distance[29]>0 && distance[29]< 19'd50000)? 1'b1:1'b0;
assign xx_reg[30] = (distance[30]>0 && distance[30]< 19'd50000)? 1'b1:1'b0;
always @ (*)
begin
if(!rst_n)
begin
xx <= 6'd32;
end
else
begin
for(i=0;i<30;i=i+1)
if(xx_reg[i]==1)
xx <= 31-i;
end
end
endmodule
直接序列解扩模块部分Verilog代码:
module test_mdecoder_2s(clk_10, rst_n, line, data_tm, en_m); //测试,最小二乘法
input clk_10, rst_n;
input signed [7:0] line;
output data_tm;
input en_m;
wire signed [30:0] distance [1:0];
wire [30:0] reg1 , reg0 ;
m_leastsquare_nl #(.KEY(5'h01)) u32(.clk_10(clk_10), .rst_n(rst_n), .line(line), .distance(distance[0]), .en_m(en_m));//0
m_leastsquare_no #(.KEY(5'h01)) u33(.clk_10(clk_10), .rst_n(rst_n), .line(line), .distance(distance[1]), .en_m(en_m));//1
assign data_tm = ( distance[1]>distance[0])? 1'b0:1'b1;//比较俩数据大小
endmodule
汉明码译码Verilog代码:
module deserialzer(clk_10, rst_n, data_tm, en_m, hdata, h_full, h_wrreq);
/* 串转并模块加汉明译码模块 */
input clk_10;
input rst_n;
input data_tm;
input en_m;
output reg [7:0] hdata;
input h_full;
output reg h_wrreq;
reg [5:0] count;
reg [2:0] bc;
reg [6:0] hdata_reg1;
reg start;
wire c0,c1,c2;
reg lh;
reg [3:0] data_reg;
/* 用来计算数据位 */
always @ (posedge clk_10)
begin
if(!rst_n)
begin
count <= 0;
bc <= 0;
end
else if(en_m && count < 30)
count <= count + 6'd1;
else
begin
if(count == 6'd30 && bc < 3'd6)
bc <= bc + 3'd1;
else
bc <= 0;
count <= 0;
end
end
/* 用来缓冲数据 */
always @ (posedge clk_10)
begin
hdata_reg1[bc] <= data_tm;
end
/* 用来控制数据写在高低位,同时控制发送写使能 */
always @ (posedge clk_10)
begin
if(!rst_n)
begin
h_wrreq <= 0;
lh <= 1;
end
else if(!h_full && bc == 3'd6 && count == 6'd30)
begin
lh <= ~lh;
if(lh)
h_wrreq <= 0;
else
h_wrreq <= 1;
end
else
h_wrreq <= 0;
end
/* 用来控制译码的使能 */
always @ (posedge clk_10)
begin
if(!rst_n)
begin
start <= 0;
end
else if(!h_full && bc == 3'd6 && count == 6'd29)
begin
start <= 1;
end
else
start <= 0;
end
assign c0 = hdata_reg1[0] ^ hdata_reg1[2] ^ hdata_reg1[4] ^ hdata_reg1[6];
assign c1 = hdata_reg1[1] ^ hdata_reg1[2] ^ hdata_reg1[5] ^ hdata_reg1[6];
assign c2 = hdata_reg1[3] ^ hdata_reg1[4] ^ hdata_reg1[5] ^ hdata_reg1[6];
/* 用来高低位数据赋值 */
always @ (*)
begin
if(lh)
hdata[7:4] <= data_reg;
else
hdata[3:0] <= data_reg;
end
always @ (posedge clk_10)
begin
if(!rst_n)
begin
data_reg <= 0;
end
else if (start)
case({c2,c1,c0})
3'b000:begin//没错误
data_reg[3] <= hdata_reg1[6];
data_reg[2] <= hdata_reg1[5];
data_reg[1] <= hdata_reg1[4];
data_reg[0] <= hdata_reg1[2];
end
3'b001:begin//校验位hc_in[0]有错误
data_reg[3] <= hdata_reg1[6];
data_reg[2] <= hdata_reg1[5];
data_reg[1] <= hdata_reg1[4];
data_reg[0] <= hdata_reg1[2];
end
3'b010:begin//校验位hc_in[1]有错误
data_reg[3] <= hdata_reg1[6];
data_reg[2] <= hdata_reg1[5];
data_reg[1] <= hdata_reg1[4];
data_reg[0] <= hdata_reg1[2];
end
3'b011:begin//校验位hc_in[0]、hc_in[1]有错误
data_reg[3] <= hdata_reg1[6];
data_reg[2] <= hdata_reg1[5];
data_reg[1] <= hdata_reg1[4];
data_reg[0] <= ~hdata_reg1[2];
end
3'b100:begin//校验位hc_in[2]有错误
data_reg[3] <= hdata_reg1[6];
data_reg[2] <= hdata_reg1[5];
data_reg[1] <= hdata_reg1[4];
data_reg[0] <= hdata_reg1[2];
end
3'b101:begin//校验位hc_in[0]、hc_in[2]有错误
data_reg[3] <= hdata_reg1[6];
data_reg[2] <= hdata_reg1[5];
data_reg[1] <= ~hdata_reg1[4];
data_reg[0] <= hdata_reg1[2];
end
3'b110:begin//校验位hc_in[1]、hc_in[2]有错误
data_reg[3] <= hdata_reg1[6];
data_reg[2] <= ~hdata_reg1[5];
data_reg[1] <= hdata_reg1[4];
data_reg[0] <= hdata_reg1[2];
end
3'b111:begin//校验位hc_in[1]、hc_in[2]、hc_in[0]有错误
data_reg[3] <= ~hdata_reg1[6];
data_reg[2] <= hdata_reg1[5];
data_reg[1] <= hdata_reg1[4];
data_reg[0] <= hdata_reg1[2];
end
endcase
end
endmodule
 芯耀
芯耀




 1796
1796

 下载ECAD模型
下载ECAD模型





