你有没有感觉做设计的时候,似乎用到的各种模型和算法都很模糊?特别是cell delay和绕线delay。本文力图消除这种模糊的感觉。
电流源模型和电压源模型
电压源,即理想电压源,是从实际电源抽象出来的一种模型,在其两端总能保持一定的电压而不论流过的电流为多少。电压源具有两个基本的性质:第一,它的端电压定值U或是一定的时间函数U(t)与流过的电流无关。第二,电压源自身电压是确定的,而流过它的电流是任意的。理想的电压源是不存在的,以电池来说,它总是有内电阻的,所获得的能量是化学反应给予的定值能量(也就是电动势)与内电阻损耗能量的差值。由于内电阻的损耗与电流有关,电流越大,损耗也越大,端电压越低,这样电池就不具有端电压定值的特点。这样我们可用理想电压源E,和电阻相串联的模型来表征实际电压源。
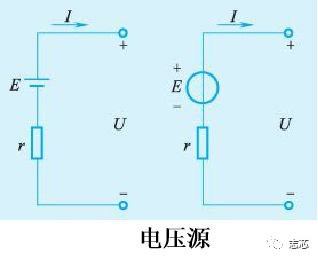
能为电路提供一定电流的电源叫电流源。实际的电流源可以用一个恒定电流I 和内阻r 并联起来的模型表示。若电源内阻r =∞,输出电流I=IS,电源始终输出恒定的电流IS。把内阻r =的电流源叫做理想电流源或恒流源。实际上,理想电流源是不存在的,因为电源内阻不可能为无穷大。
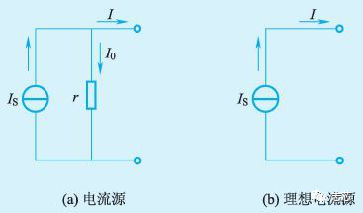
电压源以输出电压形式向负载供电,电流源以输出电流形式向负载供电。在满足一定条件下,电压源与电流源可以等效变换。等效变换是指对外电路等效,即把它们与相同的负载连接,负载两端的电压、流过负载的电流、负载消耗的功率都相同。
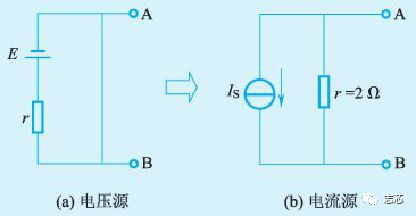
NLDM delay模型和CCS delay模型
NLDM, none lineal delay model即非线性模型,这个模型属于电压源模型。输出v不变,load上cap变化不会对电压影响。明显不适用与现在的大规模先进工艺design。已经淘汰了,米勒效应,温度的变化,高阻互联这些效应也解释不了。
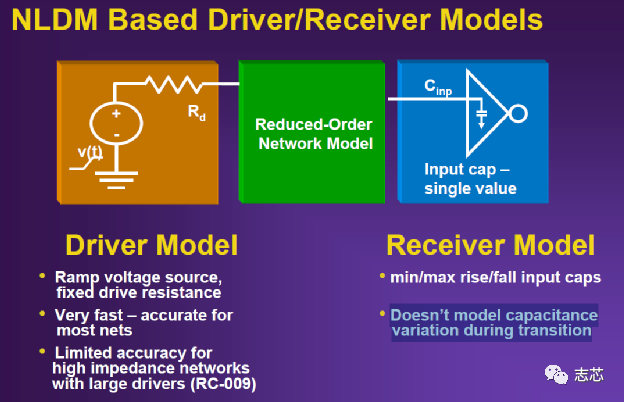
CCS,con_current source即复合电流源模型,这个模型属于电流源模型,输出I不变,load上cap变化会对I影响,V也变化。
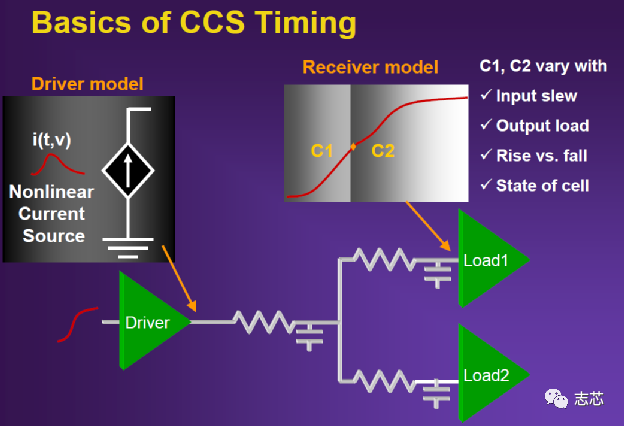
图
在给定input transition和load capacitance,NLDM得出的 cell delay具有极高的精确性,因为只有插值误差。如果input transition和load cap恰好落在查找表的格点上,得到的cell delay就是spice的仿真结果。
而对于CCS模型,在给定input transition和load capacitance下可以得到output current的波形,如果要计算出cell delay就需要重构出output voltage的波形然后再把cell delay计算出来。当然,CCS模型使用两段电容来模拟cell的input pin cap,load capacitance要比NLDM模型准确,因此CCS模型计算出的cell delay可能比NLDM模型准确。 对于计算Net delay,CCS模型中的驱动模型(随时间变化的电流源模型)肯定要比NLDM模型中的驱动模型(线性变化的电压源模型)更准确。
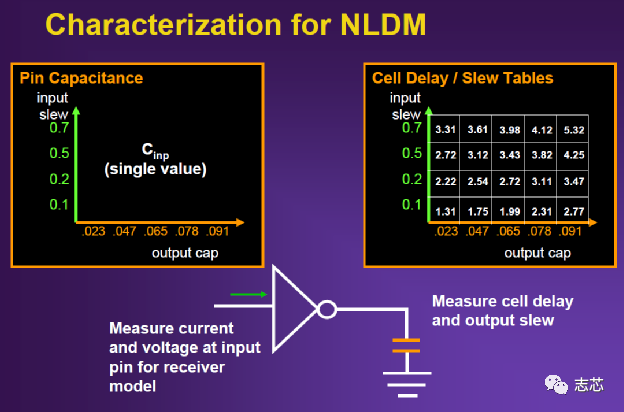

Net delay的多种计算模型
Wire Load Model
以常见的0线负载模型(Zero Wire Load Model)为例,它是根据net的扇出(fanout)来预估长度(length),然后再根据所定义的单位长度的电阻,以及单位长度电容来计算net的寄生RC参数。不过图中的例子比较理想化,都是设成了0,完全不考虑net delay。在实际项目中,必要时,可以自己定义Wire Load Model,尽量在综合阶段将Net Delay的影响考虑进去。
Elmore Delay 模型
对于单输入单输出的net,假设不考虑net之间的耦合电容(即不考虑噪声的影响),并且也不存在电阻性的反馈回路的情况,可以用Elmore Delay模型来计算Net Delay,如下图:
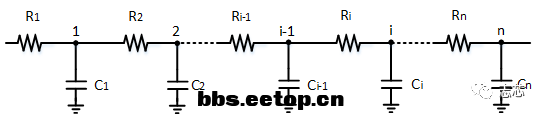
根据Elmore Delay公式,各节点的delay可以表示为:

高阶互连线延迟估计
Elmore延迟考虑的是脉冲响应的第一时刻,而AWE(渐近波形评估)、Arnoldi或其他方法能够匹配更高阶的响应时刻。通过进行更高阶的估计,可以提高计算互连线延迟的精度。
Net上的RC到底怎么算的
绕线上电阻计算公式:

其中ρ是导线的电阻率,L是导线的长度;P是导线的宽度;T是导线的厚度。
绕线上电容计算公式:
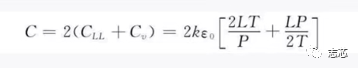
其中k是真空介电常数,ε0是真空介电常数,L是导线长度,P是导线宽度,T是导线厚度。Cll和Cv分别是导线对水平临近的导线的耦合电容和对垂直临近的导线的耦合电容。

从评估delay的角度我们基本可以认为net delay正比于导线的RC乘积。
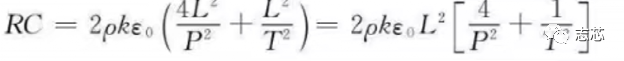
导线寄生电容计算的数学模型
现在先进工艺中越来越使用三维提取来提高寄生参数提取的精度。基本原理是使用泊松方程以及拉普拉斯方程等空间基本方程对根据版图建立的三维空间里的版图连线长度。驱动能力和负载进行计算机CAD模拟,从而得到最为精确_的模拟数据。不过工作量和计算量很大。

静电场的泊松方程和拉普拉斯方程 若空间分区充满各向同性、线性、均匀的媒质,则从静电场强与电势梯度的关系方程和高斯定理微分式,即可导出静电场的泊松方程:

式中ρ为自由电荷密度,纯数εr为各分区媒质的相对介电常数,真空介电常数εo=8.854×10-12法/米。在没有自由电荷的区域里,ρ=0,泊松方程就简化为拉普拉斯方程
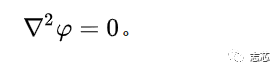
延伸思考
ccs模型是在给定input transition和load capacitance下可以得到output current的波形,如果要计算出cell delay就需要重构出output voltage的波形然后再把cell delay计算出来。这里面设计到了前一级驱动cell,后一级接收cell。在静态时序分析的时,前一级的delay的output voltage波形是已知的(这就类似于数学中的递推求解),每一级的cell delay计算其实是一个个output voltage 波形在timing path上不断传播。

所以对于drive model(就是前一级驱动cell的output voltage波形)这是一个已知条件。一个确定的output voltage波形经过具有一定的RC参数的(对于标准单元只有C),产生的曲线波形的变化和delay变化,这个过程是什么?这其实就是spice仿真,模拟电路就是这么一个一个仿真出来的。
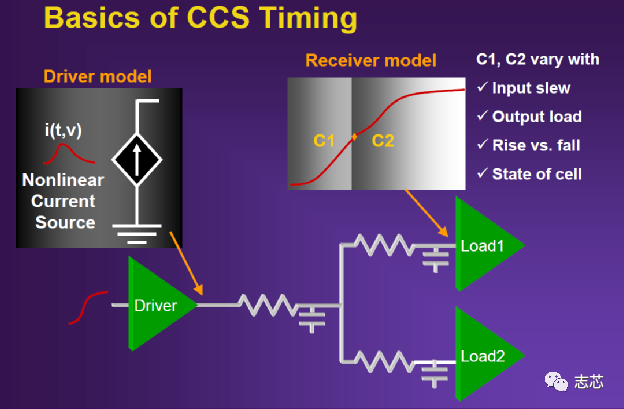
为什么receive model中的delay计算要考虑input slew?如上所述,其实对于receive cell来说 drive cell是一个已知output voltage波形,这个input slew其实就是drive cell的output voltage波形的电平变化快慢,这个会影响receive cell的电容C的计算。
为什么ccs模型中把栅极电容变成了两部分C1和C2,主要是因为要模拟米勒效应:对于MOSFET,米勒效应(Miller Effect)指其输入输出之间的分布电容(栅漏电容)在反相放大作用下,使得等效输入电容值放大的效应。由于米勒效应,MOSFET栅极驱动过程中,会形成平台电压,引起开关时间变长,开关损耗增加,给MOS管的正常工作带来非常不利的影响。
 芯耀
芯耀




 1.7万
1.7万







