dB、dBm，工程师使用分贝要谨慎

电子月

分贝早期缩写为“db”，但现在常用“dB”表示。

分贝在电子系统中的应用很常见，包括射频、音频以及现在经常提到的信号完整性。现在许多工程师都已经在用分贝思考了，但在时域领域的情况可能会不同。由于我的主要背景是射频领域，因此更倾向于将分贝与RF测量关联起来，尽管分贝最初是由电信系统工程师用来定义音频频率的。20世纪初，贝尔系统里有个概念叫做标准电缆里数（MSC，Miles of Standard Cable），用来表示一种规格为19号的电话电缆在经过一英里后的损耗特性。这个概念最后演变为传输单位（TU），定义为：

其中，Pm是测量功率，Pr是参考功率。后来，TU被命名为分贝，表示贝尔的十分之一（贝尔以Alexander Graham Bell的名字命名）。注意这支持贝尔（bel）的定义，仅表明两个功率之比的对数。TU实际上过去是一个传输单位，后来才被命名为分贝。由此人们可能很容易将分贝视为像伏特或安培这样的度量单位，但它实际上是一种用以10为底数的对数来处理两个数字比率的方法。另外，你可能注意到，分贝早期缩写为“db”，但现在常用“dB”表示。

有兴趣深入了解分贝历史的读者可以查阅American Radio History网站，该网站存档了许多经典技术出版物，包括1922年及以后的《Bell System Technical Journal》。我花了一些时间阅读早期关于电话的文章，对那时人们对电子原理的理解程度深感惊讶并自愧不如。

功率和电压

严格来讲，分贝是用于定义功率比的：

大多数工程师很快就能学会一些帮助他们进行分贝计算的经验法则，例如：

● 功率无变化，分贝值为0dB
● 功率因数为2，分贝值为+3dB或-3dB
● 功率因数为10，分贝值为+10dB或-10dB

虽然分贝被定义为功率比，但分贝公式常被用来测量电压，比如RMS（均方根）电压：

根据以上算式可以导出一个类似的公式：

在恒定阻抗（电阻）系统中，比率R1/R2的值为1，可以从等式中约除，剩下的就是我们所熟悉的电压分贝公式：

由于电气工程中的许多信号都是以电压测量的，因此将分贝应用于电压值而不是功率值会更便利。

● 电压无变化，分贝值为0dB
● 电压因数为2，分贝值为+6dB或-6dB
● 电压因数为10，分贝值为+20dB或-20dB

谨慎使用分贝

但是，忽略R1/R2项可能会导致严重混淆，因此一定要谨慎。例如，图1表示一个具有高输入阻抗（R1，100kΩ）和低输出阻抗的放大器，其驱动的负载阻抗为100Ω(R2)。输入电压为0.1VRMS，输出电压为1VRMS，电压增益为10。用分贝来表示，电压增益为20log(10)=20dB。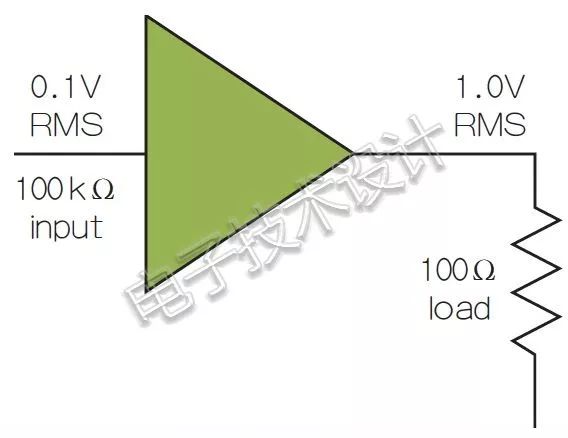

图1：具有100kΩ输入阻抗的放大器驱动100Ω负载。

再来看功率，输入功率为(0.1)²/100k=0.1µW，而负载功率为(1.0)²/100=10mW。当利用功率值计算增益时，得到10log(10mW/0.1µW)=50dB。根据我们所使用的是电压还是功率，会得出不同的放大器增益（dB）。由于电压比的分贝公式是根据功率比的分贝公式计算得出的，所以我们期望其结果也是一致的。

因为忽略了阻抗差异，我们实际上可以假定阻抗总是相同的，但在图1中情况并非如此。让我们再回头看电压方程式中的R1/R2项，计算图1中因阻抗变化缺失的因子，即10log(R1/R2)=10log(100k/100)=30dB，这个值表明了上述两个增益值之间的差异。

许多系统都具有一致的阻抗。例如，许多射频系统始终围绕50Ω系统阻抗来构建，所有输入、输出和传输线阻抗均相同。在这种情况下，功率和电压分贝方程可以互换使用，分贝值也一致。

但在其他系统中，阻抗是变化的。当然，可以使用R1/R2校正因数进行补偿，但更常见的做法是只选择电压或只选择功率来避免产生任何问题。现在，可能有纯粹主义者坚持分贝是严格按照功率来定义的（的确如此），所有分贝计算都必须考虑到这一点。我表示同意，然而我经常看到工程师们严格按照电压和20log(V2/V1)来计算而没什么问题。这样做的益处是不必调整阻抗也可以使用分贝值，但他们不得不时刻提防与功率计算混在一起。这个例子很好地说明了工程师如何有效利用数学上不纯粹却有实用价值的方法。